2023版实变函数与泛函分析课件

zhangzujin

00. 课程简介 (introduction)

00.1. 自我介绍 Introduction

---

1、 张祖锦

(1)、 高中时, 张开双臂拥抱祖国锦绣河山. 赫然写在书本上...

(2)、 工作八年后, 张氏祖传八段锦. 跟锦练八段锦

可惜了.

---

2、 1987 年生在江西兴国的一个小山村.

---

3、 2000 年高中就读于兴国平川中学. 嘿, 那时也拿到了个 全国高中数学联赛三等奖.

---

4、 2003 年本科就读于中南大学数学与应用数学专业. 学了太多计算机课程, 你看 本科时的课程与成绩 大三时也没怎么培训, 参加了湖南省首届大学生数学竞赛一等奖. 那时和同学一起做题, 大部分时候都是他先有思路, 我能完成后半段.

---

5、 2009 年中山大学硕博连读了. 其实也学了蛮多课程, 看 研究生时的课程与成绩, 期间也练了蛮多武功: 单杠挂臂后空翻 双杠仰卧起坐 悬垂慢翻上

---

6、 2012 年中山大学博士毕业. 回到了这里, 一呆啊, 就是 $\displaystyle \underline{\ \ \ \ \ \ \ \ \ \ }$ 年哦. 你看, 读书能改变命运吧, 好好读咯. 为师八年载 (更多诗词) 2019 年还有 打陀螺. 而目前啥都没了, 走走路而已.

---

7、 基本上每年都来教 实变 56 课时, 选修 $\displaystyle \to$ 必修; 现在成了 实变与泛函 72 课时, 必修 real analysis and functional analysis. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}\mbox{年年岁岁花相似, 岁岁年年人不同.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

更多介绍及课程视频等.

00.2. 回忆 Riemann 积分-数学分析

先看看 Riemann 长啥样. Riemann (18260917-18660720, Germany)

设 $\displaystyle f$ 是 $\displaystyle [a,b]$ 上的有界函数, 若对 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ T: \ a=x_0\lt x_1\lt \cdots\lt x_n=b,\\ \forall\ \xi_i\in [x_{i-1},x_i], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

都有极限 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{\left\Vert T\right\Vert \to 0} \sum_{i=1}^n f(\xi_i)(x_i-x_{i-1}) \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

存在且收敛于同一个值 $\displaystyle J$, 则称 $f$ 在 $\displaystyle [a,b]$ 上 Riemann 可积. 思想是啥? $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}\mbox{分割---求和---取极限.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

它有如下 缺陷 flaw:

---

1、 被积函数应 差不多 连续 (第 5 章我们将详细刻画, 应在除去一个 长度为 0 的集合外连续), 而 $\displaystyle [0,1]$ 上的 Dirichlet 函数 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D(x)=\left\{\begin{array}{llllllllllll} 1,&x\in[0,1]\cap \mathbb{Q}\\ 0,&x\in [0,1]\backslash\mathbb{Q} \end{array}\right.\not\in \mathscr{R}[0,1]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们将在实变函数中将可积函数类扩大, 让更多的函数可积分, 更多函数的下方图形可求面积呢.

---

2、 极限与积分交换次序的要求太严格 (一致收敛 是充分条件), 对如下 非一致收敛 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f_n(x)=x^n, x\in [0,1]\\ \Rightarrow& \lim_{n\to\infty}f_n(x)=\left\{\begin{array}{llllllllllll}0,&0\leq x\lt 1\\ 1,&x=1 \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

仍然有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}\int_0^1 f_n(x)\mathrm{ d} x=\int_0^1 \lim_{n\to\infty}f_n(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们将在实变函数中将极限与积分交换次序的要求降低到简单的验算.

---

3、 微积分基本定理的局限性: Newton-Leibnitz 公式 设 $\displaystyle f$ 在 $\displaystyle [a,b]$ 上连续, 在 $\displaystyle (a,b)$ 内可导, 且 $\displaystyle f'\in \mathscr{R} [a,b]$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_a^b f'(x)\mathrm{ d} x=f(b)-f(a). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

但是 $f'\in \mathscr{R}[a,b]$ 这一要求也太严格. 因为意大利的 Volterra 于 1881 年构造了一个函数 $\displaystyle f$, 满足 $f'$ 有界, 但 $\displaystyle f'\not\in \mathscr{R}[a,b]$. 我们将在实变函数中把 Newton-Leibnitz 公式成立的函数要求降到最低.

00.3. 构造 Lebesgue 积分-实变函数

Lebesgue (18750628-19410726, France)

实变函数的开创者 Lebesgue (勒贝格) 之传记

---

1、 Riemann 积分是对定义域进行分划, Lebesgue 积分则是对值域进行分划 (条条大路通罗马, 这条路更艰辛, 但风景这边独好): 当 $|\Delta y_i|\ll 1$ ($\ll$ 表示远远小于) 时, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \sum_i y_i \cdot \left\{x; y_{i-1}\leq f(x)\lt y_i\right\}\mbox{ 的长度} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

极限存在不? 存在的话, 就是 Lebesgue 积分! 同样是求面积, 方法不同. 浅显的说, 要数一堆面值为 $\displaystyle 1,2,5$ 毛和 $\displaystyle 1$ 元的硬币总额, Riemann 积分的思想是 一个个拿过来相加, 而 Lebesgue 积分的思想是 先将硬币整理, 面值相同的堆在一起. 宋诗也有云: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{题西林壁-苏轼}\\ \mbox{横看成岭侧成峰，远近高低各不同. }\\ \mbox{不识庐山真面目，只缘身在此山中. } \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

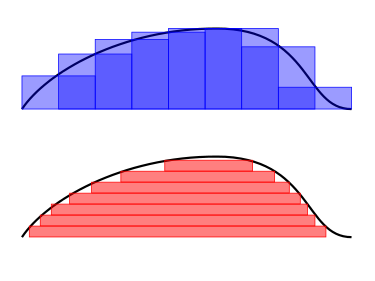上面是 Riemann 积分的思想, 下面是 Lebesgue 积分的思想

---

2、 路很艰辛, 但还是要走 (路虽远, 不行不至; 事虽难, 不为不成)! 现在的问题是如何求 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;y_{i-1}\leq f(x)\lt y_i\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

的长度. 先看个例子: 对 Dirichlet 函数而言, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;-\varepsilon\leq D(x)\lt \varepsilon\right\}=\left\{\mbox{无理数}\right\},\\ \left\{x;1-\varepsilon\leq D(x)\lt 1+\varepsilon\right\}=\left\{\mbox{有理数}\right\}; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

那么 无理数的长度 和 有理数的长度 是多少呢? 我们将在第三章中将以前所学 长度 推广为 测度 measure, 而可定义诸多集合的测度. 更多的集合可以求面积啦.

---

3、 还有泛函分析介绍呢. 这个等我们学完实变函数再说吧. 不然说了又忘记了. 本书结构如下.

(1)、 集合 (原始人)

(2)、 点集 (也称空间, 现代人, 集合 $\displaystyle +$ 某些结构

(3)、 测度论 (长度 $\displaystyle \to$ 面积 $\displaystyle \to$ 体积 $\displaystyle \to$ 测度)

(4)、 可测函数 (以前考虑连续函数, 现在考虑这个呢)

(5)、 积分论 (与数学分析相反, 我们先学积分再学微分!)

(6)、 微分与不定积分 (先学积分, 再学微分, 怪不怪?)

(7)、 度量空间和赋范线性空间 (绝对值的推广)

(8)、 有界线性算子和连续线性泛函 (线性变换/线性函数的推广)

(9)、 内积空间和希尔伯特空间 (欧氏空间的推广)

(10)、 巴拿赫空间中的基本定理 (四大基本定理)

(11)、 线性算子的谱 (嘿, 特征值的推广).

00.4. 学习实变函数与泛函分析的重要意义

---

1、 对数学分析是一种复习与加深, 应注意比较. 学后定有 会当凌绝顶, 一览众山小: 杜甫 24 岁时的狂傲 的感觉. 刚才不是看到了嘛. 数分/高代全都在脚下呢.

---

2、 学习更高深分析知识的基础, 现代分析数学基本都在 Lebesgue 的框架下讨论 (当然 Riemann 积分有用, 用来算算的啦). 第一章的 可数概念也贯穿于以后任何一门分析课程. 可以说 没有可数, 就没有现代数学.

---

3、 实际点的好处: 以前考研究生时初试要考, 现在考研究生基本都在复试中考或问. 学懂了定当 刮目相看, 区别对待. 不过国防科大可不是, 初试 150 分, 而数分和高代一共才 150 呢 国防科大的数学专业考研初试要求

---

4、 以后读了研究生, 常用 Lebesgue 积分, 时不时控制收敛 (实变的) 下, 共鸣 (泛函的) 下.

00.5. 实变函数与泛函分析的考核标准与学习方法

---

1、 本课程是必修课 (compulsory course), 是数学专业重要的基础理论和专业知识的课程.

---

2、 课前预习, 课中认真听讲, 课后独立完成作业. (2020年06月16日作) $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{历时八年, 不断凝练.}\\ \mbox{学习之前, 立下信念: }\\ \mbox{实变实变, 哪用十遍?}\\ \mbox{泛函泛函, 心不犯寒!} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

记住: 温故而知新是真理. 大家手机下载’学习通‘app, 加入班级. 用于课堂签到, 课堂考试, 课后复习等. 也记得加入课程微信群, 随时通知交流.

---

3、 建议: 多看, 多理解 (实变学十遍, 泛函不泛谈). 我读大学的时候 刘一戎老师的诗: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red} \begin{array}{c} \mbox{九问三思春复秋, 良方原在拙中求.}\\ \mbox{几多巧智随流水, 妙算从来属笨牛.} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我于 2005 年 09 月 14 日写的一首打油诗: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{新后稍前桂香飘, 回来进看实变笑.}\\ \mbox{科学高峰陡且峭, 惟有毅者登而眺.} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我于 2017 年 10 月 31 日写的一首打油诗: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{力排众难学十遍, 九问三思慢沉淀.}\\ \mbox{聪明岂是天来降, 十年一剑龙女牵.} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 尽量跟上进度, 跟不上也要把以前的知识当做常识先记起来, 多用了自然就会了. 下次再看的时候尽量补充证明. 再说了, 手机一打开, 就能看到实变与泛函的内容呢.

---

5、 孔子学琴对你定有启发.

(1)、 孔子学古琴师襄子，十日不进. 师襄子曰: “可以益矣. ”孔子曰: “丘已习其曲矣，未得其数也. ”有间，曰: “已习其数，可以益矣. ”孔子曰: “丘未得其志也. ”有间，曰: “已习其志，可以益矣. ”孔子曰: “丘未得其为人也. ”有间，有所穆然深思焉，有所怡然高望而远志焉. 曰: “丘得其为人，黯然而黑，几然而长，眼如望羊，如王四国，非文王其谁能为此也！”师襄子辟席再拜，曰: “师盖云《文王操》也. ”

(2)、 孔子向师襄子学琴，学了十天仍没有学习新曲子，师襄子对他说: “可以增加学习内容了. ”孔子说: “我已经熟悉乐曲的形式，但还没有掌握方法. ”过了一段时间，师襄子说: “你已经会弹奏的技巧了，可以增加学习内容了. ”孔子说: “我还没有领会曲子的意境. ”过了一段时间，师襄子说: “你已经领会了曲子的意境，可以增加学习内容了. ”孔子说: “我还不了解作者. ”又过了一段时间，孔子神情俨然，仿佛进到新的境界: 时而神情庄重穆然，若有所思，时而怡然高望，志意深远；孔子说: “我知道他是谁了: 那人皮肤深黑，体形颀长，眼光明亮远大，像个统治四方诸侯的王者，若不是周文王还有谁能撰作这首乐曲呢？”师襄子听到后，赶紧起身拜了两拜，回答道: “老琴师传授此曲时就是这样说的，这支曲子叫做《文王操》啊！”

01. 集合 (set)

01.1. 集合的表示

---

1、 集合 (set) 的定义: 若干事物的全体 (朴素的语言)

---

2、 常用集合的符号.

(1)、 $\displaystyle \mathbb{N}$ 自然数集合 (natural numbers);

(2)、 $\displaystyle \mathbb{Z}$ 整数集合 (Zahlen 德语);

(3)、 $\displaystyle \mathbb{Q}$ 有理数集合 (quotients);

(4)、 $\displaystyle \mathbb{R}$ 实数集合 (real numbers);

(5)、 $\displaystyle \mathbb{C}$ 复数集合 (complex numbers).

---

3、 集合的表示法 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{\begin{array}{llllllllllll} \mbox{列举法: } \mathbb{N}=\left\{0,1,2,3,\cdots\right\};\\ \mbox{特征性质描述法: }A=\left\{x; P(x)\mbox{ 成立}\right\}.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red} \boxed{x\in A\Leftrightarrow P(x)\mbox{成立.}} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 包含关系. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\subset B&\stackrel{\rm def}{\Leftrightarrow}\left[\forall\ x\in A,\mbox{ 有 }x\in B\right]\\ &\Leftrightarrow \left[x\in A\Rightarrow x\in B\right]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mbox{$f: [a,b]\to \mathbb{R}$ 有上界 $\displaystyle M$}\\ \Leftrightarrow&\mbox{$\forall\ x\in[a,b]$, 有 $f(x)\leq M$}\\ \Leftrightarrow&\forall\ x\in [a,b], x\in \left\{x; f(x)\leq M\right\}\\ \Leftrightarrow&\mbox{$[a,b]\subset \left\{x;f(x)\leq M\right\}.$} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 例. $f$ 在 $\displaystyle x_0$ 处连续等价于 $\displaystyle \forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\mathrm{ s.t.} \forall\ x\in (x_0-\delta,x_0+\delta)$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &|f(x)-f(x_0)|\lt \varepsilon\\ \Leftrightarrow&f(x)\in (f(x_0)-\varepsilon,f(x_0)+\varepsilon)\\ \Leftrightarrow&x\in f^{-1\left(\left(f(x_0)-\varepsilon,f(x_0)+\varepsilon\right)\right)}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

对 $f: X\to Y$, $B\subset Y$, 定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}f^{-1}(B)=\left\{x\in X;\ f(x)\in B\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}\boxed{x\in f^{-1}(B)\Leftrightarrow f(x)\in B.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

总结起来, $f$ 在 $\displaystyle x_0$ 处连续等价于 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall \varepsilon\gt 0,\exists\ \delta\gt 0,\mathrm{ s.t.}\\ &(x_0-\delta,x_0+\delta)\subset f^{-1}\left(\left(f(x_0)-\varepsilon,f(x_0)+\varepsilon\right)\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 集合相等. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A=B&\stackrel{\rm def}{\Leftrightarrow} \left[A\subset B,\ B\subset A\right]\\ &\Leftrightarrow \left[x\in A\Leftrightarrow x\in B\right]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

8、 例. 设 $\displaystyle f$ 在 $\displaystyle [a,b]$ 上连续, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f([a,b])=[m,M],\mbox{ 其中 } \left\{\begin{array}{llllllllllll} m=\inf_{[a,b]}f,\\ M=\sup_{[a,b]}f. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2. 集合的运算

01.2.1. 集族

---

1、 设 $\displaystyle \varLambda$ 是一个集合, 对 $\displaystyle \forall\ \lambda\in \varLambda$, 都指定一个集合 $A_\lambda$, 则称 $\left\{A_\lambda\right\}_{\lambda\in \varLambda}$ 为一个集族 (family). 当 $\displaystyle \varLambda=\mathbb{Z}_+$ 时, 则称其为一个集列, 记作 $\displaystyle \left\{A_k\right\}_{k=1}^\infty$.

(1)、 集族 $\left\{A_\lambda\right\}_{\lambda\in\varLambda}$ (类比家族). $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \varLambda\ni \lambda\mapsto A_\lambda. \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 集列 $\displaystyle \left\{A_k\right\}_{k=1}^\infty$ (类比数列, 函数列及由人组成的 $\displaystyle \underline{\ \ \ \ \ \ \ \ \ \ }$). $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{Z}_+\ni k\mapsto A_k. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{赠卫八处士-杜甫}\\ \mbox{人生不相见, 动如参与商. } \mbox{今夕复何夕, 共此灯烛光. }\\ \mbox{少壮能几时, 鬓发各已苍. } \mbox{访旧半为鬼, 惊呼热中肠. }\\ \mbox{焉知二十载, 重上君子堂. } \mbox{昔别君未婚, 儿女忽成行. }\\ \mbox{怡然敬父执, 问我来何方. } \mbox{问答乃未已, 儿女罗酒浆. }\\ \mbox{夜雨翦春韭, 新炊间黄粱. } \mbox{主称会面难, 一举累十觞. }\\ \mbox{十觞亦不醉, 感子故意长. } \mbox{明日隔山岳, 世事两茫茫. } \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.2. 并集 (union)

---

1、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcup_{\lambda\in \varLambda}A_\lambda \stackrel{\rm def}{=}\left\{x;\exists\ \lambda\in \varLambda,\mathrm{ s.t.} x\in A_\lambda\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

从而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}x\in \bigcup_{\lambda\in \varLambda}A_\lambda\Leftrightarrow \exists\ \lambda\in \varLambda,\mathrm{ s.t.} x\in A_\lambda. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 基本性质. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ \lambda_0\in \varLambda,\ A_{\lambda_0}\subset \bigcup_{\lambda\in \varLambda}A_\lambda \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A_n=\left\{\frac{m}{n};m\in\mathbb{Z}\right\},\quad \bigcup_{n=1}^\infty A_n=\mathbb{Q} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. 无穷多个闭区间并起来可以是一个开区间呢. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcup_{n=1}^\infty \left[a+\frac{1}{n},b-\frac{1}{n}\right]=(a,b). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 例. 左端每个集合中函数有正下界! 集合分解很重要的啦. 实变函数是用集合语言来说话. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcup_{n=1}^\infty \left\{x;f(x)\gt \frac{1}{n}\right\}=\left\{x;f(x)\gt 0\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.3. 交集 (intersection)

---

1、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcap_{\lambda\in \varLambda}A_\lambda \stackrel{\rm def}{=}\left\{x;\forall\ \lambda\in\varLambda,\mbox{ 有 }x\in A_\lambda\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}\boxed{x\in \bigcap_{\lambda\in \varLambda}A_\lambda\Leftrightarrow \forall\ \lambda\in\varLambda,\ x\in A_\lambda.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 基本性质. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ \lambda_0\in\varLambda,\ \bigcap_{\lambda\in \varLambda}A_\lambda\subset A_{\lambda_0}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcap_{n=1}^\infty\left(a-\frac{1}{n},b+\frac{1}{n}\right)=[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. 设 $f_n$ 是 $\displaystyle E$ 上的函数列, 则对 $\displaystyle \forall\ c\in\mathbb{R}$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;\sup_nf_n(x)\leq c\right\}&=\bigcap_{n=1}^\infty\left\{x;f_n(x)\leq c\right\};\\ \left\{x;\inf_nf_n(x)\lt c\right\}&=\bigcup_{n=1}^\infty \left\{x;f_n(x)\lt c\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.4. 交并运算律、De Morgan 律及其他

---

1、 交换律 (commutativity): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\cup B=B\cup A, \quad A\cap B=B\cap A. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 结合律 (associativity): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (A\cup B)\cup C=A\cup (B\cup C),\\ (A\cap B)\cap C=A\cap(B\cap C). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 分配律 (distributivity): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\cup(B\cap C)=(A\cup B)\cap(A\cup C),\\ A\cap(B\cup C)=(A\cap B)\cup(A\cap C). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 幂等律 (idempotency): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\cup A=A,\quad A\cap A=A. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 差 (difference), 补 (complement): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\backslash B&\stackrel{\rm def}{=}\left\{x;x\in A,x\not\in B\right\},\\ A^c&\stackrel{\rm def}{=}\left\{x\in S;x\not\in A\right\}\ \left(S\mbox{ 是全集}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 一个常用公式 把差运算变成我们熟悉的交运算呢. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\backslash B=A\cap B^c. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 De Morgan 律 (记忆大师: 交的补=补的并, 并的补=补的交). $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left(\bigcap_{\lambda\in \varLambda}A_\lambda\right)^c &=\bigcup_{\lambda\in \varLambda}A_\lambda^c;\\ \left(\bigcup_{\lambda\in \varLambda}A_\lambda\right)^c &=\bigcap_{\lambda\in \varLambda}A_\lambda^c. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.5. 数学语言的集合表示

---

1、 关键点 (Key points): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{存在}\Leftrightarrow\mbox{并运算},\\ \mbox{任意}\Leftrightarrow\mbox{交运算}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. 若 $\lim_{n\to\infty}a_n=a$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{a\right\}=\bigcap_{k=1}^\infty \bigcup_{N=1}^\infty\bigcap_{n=N}^\infty \left(a_n-\frac{1}{k},a_n+\frac{1}{k}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;\left\{f_n(x)\right\}\mbox{ 有界}\right\} =\bigcup_{k=1}^\infty\bigcap_{n=1}^\infty \left\{x;|f_n(x)|\leq k\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{x;\lim_{n\to\infty}f_n(x)=0\right\}\\ =&\bigcap_{k=1}^\infty \bigcup_{N=1}^\infty \bigcap_{n=N}^\infty \left\{x;|f_n(x)|\lt \frac{1}{k}\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 思考题. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;\left\{f_n(x)\right\}\mbox{ 无界}\right\}&=?\\ \left\{x;\lim_{n\to\infty}f_n(x)\mbox{ 不存在或存在但 }\neq 0\right\}&=? \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.6. 上、下极限集

设 $\left\{A_n\right\}$ 是一集列.

---

1、 定义. $\displaystyle \left\{A_n\right\}$ 的上限集 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \varlimsup_{n\to\infty}A_n\\ &\stackrel{\rm def}{=}\left\{x;\mbox{存在无穷多个 }n,\mbox{ 使得 }x\in A_n\right\}\\ &=\left\{x;x\mbox{常在} A_n\right\}\left(\mbox{名曰: 柳常在, 正如恋爱}\right)\\ &=\left\{x;\exists\ \left\{n_k\right\},\mathrm{ s.t.} x\in A_{n_k}\right\}\\ &=\left\{x;\forall\ n\in\mathbb{Z}_+,\ \exists\ m\gt n,\mathrm{ s.t.} x\in A_m\right\}\\ &=\bigcap_{n=1}^\infty\bigcup_{m=n}^\infty A_m. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 定义. $\displaystyle \left\{A_n\right\}$ 的下限集 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \varliminf_{n\to\infty}A_n\\ &\stackrel{\rm def}{=}\left\{x;\mbox{当 }n\mbox{ 充分大时}, x\in A_n\right\}\\ &=\left\{x;x\mbox{终在} A_n\right\}\left(\mbox{名曰: 柳终在, 正如婚姻}\right)\\ &=\left\{x;\exists\ n\in\mathbb{Z}_+,\ \forall\ m\gt n,\mbox{ 有 } x\in A_m\right\}\\ &=\bigcup_{n=1}^\infty\bigcap_{m=n}^\infty A_m. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 基本性质. 一直在定终在, 终在定常在, 常在定偶偶在. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcap_{n=1}^\infty A_n\subset \varliminf_{n\to\infty}A_n \subset \varlimsup_{n\to\infty}A_n \subset \bigcup_{n=1}^\infty A_n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{a\right\}&=\bigcap_{k=1}^\infty \bigcup_{N=1}^\infty\bigcap_{n=N}^\infty \left(a_n-\frac{1}{k},a_n+\frac{1}{k}\right)\\ &=\bigcap_{k=1}^\infty \varliminf_{n\to\infty}\left(a_n-\frac{1}{k},a_n+\frac{1}{k}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 例. 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A_{2m+1}&=\left[0,2-\frac{1}{2m+1}\right],\quad m=0,1,2,\cdots;\\ A_{2m}&=\left[0,1+\frac{1}{2m}\right],\quad m=1,2,3,\cdots. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

求 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \varlimsup_{n\to\infty}A_n,\ \varliminf_{n\to\infty}A_n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 集列极限存在的定义 类比数列极限. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}A_n\mbox{ 存在} \stackrel{\rm def}{\Leftrightarrow} \varliminf_{n\to\infty}A_n=\varlimsup_{n\to\infty}A_n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.7. 单调集列

设 $\displaystyle \left\{A_n\right\}$ 是一集列.

---

1、 若 $\displaystyle \varliminf_{n\to\infty}A_n=\varlimsup_{n\to\infty}A_n$, 则称集列 $\left\{A_n\right\}$ 收敛, 记为 $\displaystyle \lim_{n\to\infty}A_n$.

---

2、 若 $A_1\subset A_2\subset A_3\subset\cdots$, 则称 $\left\{A_n\right\}$ 为单增集列.

---

3、 若 $\displaystyle A_1\supset A_2\supset A_3\supset\cdots$, 则称 $\left\{A_n\right\}$ 为单减集列.

---

4、 单调有界定理

(1)、 若 $\displaystyle A_n$ 单增, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}A_n=\bigcup_{n=1}^\infty A_n; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 若 $\displaystyle A_n$ 单减, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}A_n=\bigcap_{n=1}^\infty A_n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x;f(x)\gt 0\right\} &=\bigcup_{n=1}^\infty \left\{x;f(x)\gt \frac{1}{n}\right\}\\ &=\lim_{n\to\infty}\left\{x;f(x)\gt \frac{1}{n}\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.2.8. 集合的直积 (Cartesian product)

---

1、 定义. 设 $\displaystyle \left\{A_i\right\}_{i=1}^n$ 是集合, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \prod_{i=1}^n A_i=&A_1\times \cdots\times A_n\\ =&\left\{(a_1,\cdots,a_n);a_i\in A_i\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle A_1,\cdots,A_n$ 的直积; 类似的, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \prod_{i=1}^\infty A_i &=\left\{(a_1,\cdots,a_n,\cdots);a_i\in A_i\right\},\\ A^n&=\underbrace{A\times A\times\cdots\times A}_{n\mbox{ 个}}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{R}^n&=\left\{(x_1,\cdots,x_n); x_k\in \mathbb{R}\right\},\\ \mathbb{R}^\infty &=\left\{x=\left\{x_k\right\}_{k=1}^\infty=(x_1,x_2,\cdots);x_k\in\mathbb{R}\right\}\\ &\left(\mbox{实数列全体}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.3. 对等 (equipotency) 与基数 (cardinal)

01.3.1. 对等的定义

---

1、 集合按照元素的个数可以分为有限集与无限集. 有限集有个数的概念: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &A,B\mbox{ 个数相同}\\ \Leftrightarrow& A,B\mbox{ 之间有一个一一对应 (bijection)}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 思考. 无限集呢? 当然, 你会说无限集有无限多个元素, 没错. 但如何比较元素个数的多少?

---

3、 对无限集而言, 我们可以推广得到: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ A,B\mbox{ 基数相同}\quad \left(\mbox{记作: }\overline{\overline{A}}=\overline{\overline{B}}\right)\\ &\stackrel{\rm def}{\Leftrightarrow} A,B\mbox{ 对等}\quad \left(\mbox{记作: }A\sim B\right)\\ &\stackrel{\rm def}{\Leftrightarrow} A,B\mbox{ 之间存在一个一一对应 (bijection)}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.3.2. 对等的例子

---

1、 正奇数集合、正偶数集合、整数集都与自然数集对等, 基数相同.

---

2、 $\displaystyle (-1,1)\sim \mathbb{R}$.

---

3、 两个同心圆对等.

传统的, $A\subset B$ 我们理解为: $\displaystyle B$ 的元素会更多. 现代的, Cantor 说: 不行. $\displaystyle A\subset B$, 但 $B$ 的个数 (基数) 更多. Cantor 的突破当然也引起了轩然大波...

01.3.3. 对等的性质

---

1、 自反性 (reflexivity): $\displaystyle A\sim A$;

---

2、 对称性 (symmetry): $A\sim B\Rightarrow B\sim A$;

---

3、 传递性 (transitivity): $A\sim B, B\sim C\Rightarrow A\sim C$.

这表明集合的对等是一个等价关系 (equivalence relation, 近世代数/点集拓扑课程都会讲的啊).

01.3.4. 基数的比较

---

1、 思考. $\mathbb{R}$ 中有 $\displaystyle \lt$, $=$, $\gt$ 关系 (任意两个数 $\displaystyle a,b$, $a\lt b,a=b,a\gt b$ 三者必居其一且仅居其一), 集合的基数是否可以比较呢, 也有类似的性质么?

---

2、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A}}\lt \overline{\overline{B}}\stackrel{\rm def}{\Leftrightarrow}\left\{\begin{array}{ll} A,B\mbox{ 不对等}\\ A\mbox{ 与 }B\mbox{ 的某个真子集 }B^\star \mbox{ 对等} \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 推论: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A}}\leq \overline{\overline{B}}&\stackrel{\rm def}{\Leftrightarrow} \left\{\begin{array}{llllllllllll} \overline{\overline{ A}}\lt \overline{\overline{ B}}\\ \mbox{或}\overline{\overline{ A}}=\overline{\overline{ B}} \end{array}\right.\\ &\Leftrightarrow A\mbox{ 与 }B\mbox{ 的某个子集 }B^\star \mbox{ 对等}\\ &\Leftrightarrow A\sim \underline{B^\star }\subset B. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 对任何 $\displaystyle A,B$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A}}&\lt \overline{\overline{B}},\\ \overline{\overline{A}}&=\overline{\overline{B}},\\ \overline{\overline{A}}&\gt \overline{\overline{B}} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

三者必居其一且仅居其一.

---

5、 思考. $\mathbb{R}$ 中有 $\displaystyle a\leq b,b\leq a\Rightarrow a=b$, 集合的包含关系有 $A\subset B,B\subset A\Rightarrow A=B$. 对集合的基数而言有类似的关系么?

---

6、 Bernstein 定理. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A}}\leq \overline{\overline{B}},\quad \overline{\overline{B}}\leq \overline{\overline{A}}\Rightarrow \overline{\overline{A}}=\overline{\overline{B}}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red} &\mbox{用 Bernstein 定理就是做填空题: }\\ &\left.\begin{array}{rrrr} A\sim\underline{\ \ \ \ \ \ \ \ \ \ } \subset B\\ B\sim\underline{\ \ \ \ \ \ \ \ \ \ } \subset A \end{array}\right\}\Rightarrow A\sim B. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 例 类比数列极限的夹逼原理, 我们称之为迫对等性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{rrrr} A\subset B\subset C\\ A\sim C\end{array}\right\} \Rightarrow A\sim B\sim C. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

8、 例. 所有 (开、闭、半开半闭、无穷) 区间均与 $\mathbb{R}$ 对等.

---

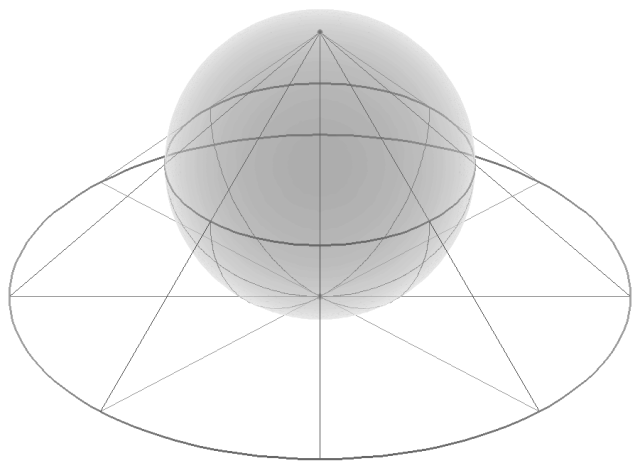
9、 例. $\displaystyle \mathbb{R}^3$ 中的单位球面 (地球仪) 去掉北极点与平面 $\displaystyle \mathbb{R}^2$ (墙上地图) 通过球极投影 (Stereographic projection)一一对应.

01.4. 可数集合 (countable set)

01.4.1. 定义与初步例子

---

1、 定义: 若 $\displaystyle A\sim\mathbb{Z}_+$, 则称 $A$ 为可数集 (countable set).

---

2、 例. 正奇数集合、正偶数集合、整数集合.

01.4.2. 可数集的性质

---

1、 任何无限集均有一个可数子集. 即: 若 $\displaystyle A$ 为无限集, 则 $\displaystyle \overline{\overline{A}}\gt a\stackrel{\rm def}{=}\overline{\overline{\mathbb{Z}_+}}$.

---

2、 可数集的任何无限子集为可数集, 可数集的任何子集为有限集或可数集.

---

3、 $A$ 可数, $\displaystyle B$ 至多可数 (即: 有限或可数), 则 $\displaystyle A\cup B$ 可数.

---

4、 $\displaystyle \left\{A_i\right\}_{i=1}^n$ 至多可数, 则 $\displaystyle \bigcup_{i=1}^n A_i$ 也至多可数; 且若某 $\displaystyle A_i$ 可数, 则 $\displaystyle \bigcup_{i=1}^n A_i$ 可数.

---

5、 $\displaystyle \left\{A_i\right\}_{i=1}^\infty$ 为可数集列, 则 $\displaystyle \bigcup_{i=1}^\infty A_i$ 可数 (可数个可数集并起来还可数).

---

6、 $\displaystyle \left\{A_i\right\}_{i=1}^n$ 可数, 则 $\displaystyle \prod_{i=1}^n A_i$ 可数.

---

7、 $\displaystyle f: X\to Y$ 是单射, $\displaystyle Y$ 可数, 则 $\displaystyle X$ 至多可数.

---

8、 $\displaystyle X$ 可数, $\displaystyle f: X\to Y$ 是满射, 则 $\displaystyle Y$ 至多可数.

01.4.3. 进一步的例子

---

1、 $\displaystyle \mathbb{Q}$ 可数.

---

2、 直线上互不相交的开区间族至多可数

---

3、 $\displaystyle \mathbb{Q}^2$ ($\mathbb{R}^2$ 中有理点全体) 可数.

---

4、 整系数多项式全体 $\displaystyle \mathbb{Z}[x]$ 可数.

---

5、 代数数全体 $\displaystyle A$ 可数.

01.5. 不可数集合 (uncountable set)

01.5.1. 定义与例子

---

1、 定义: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{集合}\left\{\begin{array}{ll} \mbox{有限集}\\ \mbox{无限集}\left\{\begin{array}{ll} \mbox{可数集}\\ \mbox{不可数集}: \mbox{不是可数集的无限集} \end{array}\right. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle \mathbb{R}$ 不可数.

(1)、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mbox{两个小数相等 $\displaystyle \Leftrightarrow$ 小数点后任一位的数字相等,}\\ &\mbox{两个小数不等 $\displaystyle \Leftrightarrow \exists$ 小数点后某一位的数字不等!} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 著名的 Cantor 对角线法 (Cantor diagonal method).

01.5.2. 连续基数的性质

---

1、 以 $\displaystyle c$ 表示 $\displaystyle \mathbb{R}$ 的基数 (称为连续基数), 则上例给出 $\displaystyle \overline{\overline{\mathbb{R}}}=c\gt a=\overline{\overline{\mathbb{N}}}$.

---

2、 由 Bernstein 定理, 所有的 (开、闭、半开半闭、无穷) 区间都基数 $c$.

---

3、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A_n}}=c\Rightarrow \overline{\overline{\bigcup_{n=1}^\infty A_n}}=c. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A_n}}=c\Rightarrow \overline{\overline{\prod_{n=1}^\infty A_n}}=c. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 实数列全体 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{R}^\infty=\left\{(a_1,a_2,\cdots);a_i\in\mathbb{R}\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

具有连续基数.

---

6、 $\mathbb{R}^n (n\gt 1)$ 具有连续基数.

---

7、 $\displaystyle 0-1$ 数列全体 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{0,1\right\}^\infty= \left\{(a_1,a_2,\cdots);a_i=0\mbox{ 或 }1\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

具有连续基数.

---

8、 可数集 $\displaystyle A$ 的所有子集构成的集族 $\displaystyle 2^A$ 的基数为 $\displaystyle c$.

---

9、 整数列全体 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{Z}^\infty=\left\{(a_1,a_2,\cdots);a_n\in\mathbb{Z}\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

具有连续基数.

---

10、 $c$ 个具有连续基数的集的并的基数为 $\displaystyle c$: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\overline{A_\lambda}}=c,\ \forall\ \lambda\in \varLambda,\quad \overline{\overline{\varLambda}}=c\Rightarrow \overline{\overline{\bigcup_{\lambda\in \varLambda}A_\lambda}}=c. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

01.5.3. 无最大基数定理

---

1、 思考: 有没有最大的基数?

---

2、 无最大基数定理: 设 $M$ 是一个集合, $\displaystyle \mu$ 为 $\displaystyle M$ 的所有子集构成的集族, 则 $\displaystyle \overline{\overline{M}}\lt \overline{\overline{\mu}}$.

01.6. 本章小结

---

1、 集合

(1)、 概念, 表示方法, 运算 (并, 交, 差, 补) 及其性质 (比如 De Morgan 公式, 这是对偶律).

(2)、 数学语言的集合表示.

(3)、 集列的上极限, 下极限和极限.

---

2、 对等, 基数

(1)、 概念, 例子.

(2)、 Bernstein 定理.

---

3、 可数集, 不可数集

(1)、 可数集的概念, 例子, 性质.

(2)、 不可数集的概念, 例子, 性质.

02. 点集 (point set)

02.1. 度量空间 (metric space), $n$ 维 Euclidean 空间

02.1.1. 度量空间的定义与例子

---

1、 回忆: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\lim_{n\to\infty}a_n=a\\ \stackrel{\rm def}{\Leftrightarrow}&\forall\ \varepsilon\gt 0,\ \exists\ N,\ \forall\ n\gt N,\mbox{ 有 }|a_n-a|\lt \varepsilon. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\displaystyle \mathbb{R}$ 中有 距离 (可以衡量两数的接近程度, 这里是绝对值) 的概念, 就可以定义极限.

---

2、 设 $\displaystyle X$ 是一个集合, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{ccccc} d: &X\times X&\to&[0,\infty)\\ &(x,y)&\mapsto&d(x,y) \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 正定性 (positivity): $\displaystyle d(x,y)\gt 0$, $d(x,y)=0\Leftrightarrow x=y$, $\forall\ x,y\in X$;

(2)、 对称性 (symmetry): $d(x,y)=d(y,x)$, $\forall\ x,y\in X$;

(3)、 三角不等式 (triangle inequality): $d(x,y)\leq d(x,z)+d(z,y),\ \forall\ x,y,z\in X$;

则称 $d$ 为 $\displaystyle X$ 上的一个距离 (distance), $\displaystyle (X,d)$ 称为 度量空间 (metric space).

---

3、 课外延展 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{rrrr} \mbox{对称性}\\ \mbox{三角不等式} \end{array}\right\}\Leftrightarrow \boxed{\begin{array}{c}d(x,y)\leq d(x,z)+d(y,z),\\ \forall\ x,y,z\in X.\end{array}} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 度量子空间. 若 $\displaystyle (X,d)$ 是度量空间, $\displaystyle \varnothing \neq Y\subset X$, 则 $(Y,d|_{Y\times Y})$ 是度量空间, 称为 $\displaystyle (X,d)$ 的子空间. 比较:

(1)、 线性子空间: 子集在加法与数量乘法运算下封闭;

(2)、 线性变换的限制 $\displaystyle \mathscr{A}|_W$;

(3)、 子群, 子环等;

(4)、 度量子空间: 子集中的两个点也有距离嘛.

---

5、 例. 在 $\mathbb{R}^n$ 中, 对 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x=(x_1,\cdots,x_n),\quad y=(y_1,\cdots,y_n), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\left[\sum_{i=1}^n (x_i-y_i)^2\right]^{1/2}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle (\mathbb{R}^n,d)$ 为度量空间, 称为 $\displaystyle n$ 维 Euclidean 空间, $\displaystyle d$ 称为 Euclidean 距离.

02.1.2. 邻域、极限及其它

设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle x_0\in X$, $A,B,E\subset X$.

---

1、 邻域 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} U(x_0;\delta)&=U(x_0)\\ &\stackrel{\rm def}{=}\left\{x\in X; d(x,x_0)\lt \delta\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 极限 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \lim_{n\to\infty}x_n=x_0\\ &\stackrel{\rm def}{\Leftrightarrow} \forall\ \varepsilon\gt 0,\ \exists\ N,\ \forall\ n\gt N, 0\leq a_n=d(x_n,x_0)\lt \varepsilon\\ &\Leftrightarrow \lim_{n\to\infty}a_n=0\\ &\Leftrightarrow \lim_{n\to\infty}d(x_n,x_0)=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

度量空间中点列的极限通过距离函数转化成了数列极限!!

---

3、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{两集合的距离: }d(A,B)&\stackrel{\rm def}{=}\inf_{x\in A,y\in B}d(x,y);\\ \mbox{集合的直径: }\delta(A)&\stackrel{\rm def}{=}\sup_{x\in A,\ y\in A}d(x,y). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

引导: 平面上点 $p$ 到直线 $\displaystyle L$ 的距离; 圆的直径. 画个图来.

---

4、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\mbox{ 有界}&\stackrel{\rm def}{\Leftrightarrow} \delta(A)\lt \infty\quad \left(\mbox{度量空间中}\right)\\ &\Leftrightarrow \exists\ R\gt 0,\ \forall\ x\in A,\ d(x,x_0)\leq R. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 $\displaystyle n$ 维开、闭区间为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \prod_{i=1}^n (a_i,b_i),\quad \prod_{i=1}^n [a_i,b_i], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

它们都有 体积 $\displaystyle \prod_{i=1}^n (b_i-a_i)$.

02.2. 聚点 (cluster point), 内点 (interior point), 界点 (boundary point)

02.2.1. 点与集的第一类关系: 内点, 外点, 聚点

设 $E\subset \mathbb{R}^n, x_0\in \mathbb{R}^n$.

---

1、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ U(x_0)\subset E, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $x_0$ 为 $\displaystyle E$ 的内点 (interior point); $\displaystyle E$ 的全体内点所成集合称为 $\displaystyle E$ 的开核, 记作 $\displaystyle E^\circ$.

---

2、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ U(x_0)\subset E^c\Leftrightarrow x_0\in E^{c\circ}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $x_0$ 为 $\displaystyle E$ 的外点 (exterior point). $\displaystyle E$ 的外点全体为 $\displaystyle E^{c\circ}$. 不用再给个记号啦.

---

3、 若 $x_0$ 既不是 $\displaystyle E$ 的内点, 也不是 $\displaystyle E$ 的外点, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ U(x_0),\ \left\{\begin{array}{llllllllllll} U(x_0)\not\subset E\Leftrightarrow U(x_0)\cap E^c\neq\varnothing\\ U(x_0)\not\subset E^c\Leftrightarrow U(x_0)\cap E\neq \varnothing\end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

此时, 称 $\displaystyle x_0$ 为 $\displaystyle E$ 的界点 (boundary point); 全体界点所成集合称为 $\displaystyle E$ 的边界, 记作 $\displaystyle \partial E$. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\subset B&\Leftrightarrow [x\in A\Rightarrow x\in B\Leftrightarrow x\not \in B^c]\\ &\Leftrightarrow A\cap B^c=\varnothing, \therefore \boxed{A\not\subset B\color{red\Leftrightarrow A\cap B^c\neq \varnothing}}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 总结: $x_0$ 与 $\displaystyle E$ 的关系必有且仅有 内点、外点、界点 这三种.

02.2.2. 点与集的第二类关系: 聚点, 孤立点和外点

---

1、 刚才我们看的是 $\displaystyle x_0$ 的邻域是否完全落在 $\displaystyle E$ 或 $\displaystyle E^c$上, 我们现在看 $x_0$ 的去心邻域是否与 $\displaystyle E$ 有交. 这一性质对研究函数的极限很重要. 回忆二元函数极限的定义 比如: 设 $\displaystyle f(x)$ 是 $\displaystyle E\subset \mathbb{R}^2$ 上的函数, $\displaystyle x_0$ 是 $\displaystyle E$ 的 $\displaystyle \underline{\ \ \ \ \ \ \ \ \ \ }$, $A\in\mathbb{R}$. 若 $\forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\mathrm{ s.t.}$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in E\cap U(x_0;\delta)\backslash\left\{x_0\right\}\Rightarrow f(x)\in U(A;\varepsilon), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle f$ 在 $\displaystyle x_0$ 处极限存在. 这就要求 $\displaystyle \boxed{\forall\ \delta\gt 0,\ E\cap U(x_0;\delta)\backslash \left\{x_0\right\}\neq \varnothing}$. 否则如何谈函数极限: 当 $x\to x_0$ 时, 函数值的变化趋势.

---

2、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ U(x_0),\quad U(x_0)\cap (E\backslash \left\{x_0\right\})\neq \varnothing, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle x_0$ 为 $\displaystyle E$ 的聚点 (cluster point); $\displaystyle E$ 的全体聚点所成集合称为 $\displaystyle E$ 的导集 (derived set), 记作 $\displaystyle E'$.

---

3、 $E\cup E'$ 称为 $\displaystyle E$ 的闭包 (closure), 记作 $\displaystyle \bar{E}$ 或 $\displaystyle E^-$, $E^-$ 中的点称为 $\displaystyle E$ 的极限点 (limit point). 为啥考虑闭包? 看例子: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &E=(1,2)\cup \left\{3\right\}\Rightarrow E'=[1,2]\\ \Rightarrow&\mbox{怎么搞的? 孤立点 (岛) $\displaystyle 3\in E$, 求’导‘后怎么可以丢呢?}\\ \Rightarrow&\mbox{所以考虑 $\bar{E}=E\cup E'$, 领土神圣, 不可丢失!} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 若 $x_0$ 不是 $\displaystyle E$ 的聚点, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ U(x_0),\mathrm{ s.t.} &U(x_0)\cap E\cap \left\{x_0\right\}^c=\varnothing\\ \Rightarrow& U(x_0)\cap E\subset \left\{x_0\right\}.\\ &\color{red} A\cap B^c=\varnothing\Leftrightarrow A\subset B. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而只有两种情形,

(1)、 若 $\displaystyle U(x_0)\cap E=\left\{x_0\right\}$, 则称 $x_0$ 为 $\displaystyle E$ 的孤立点 (isolated point).

(2)、 若 $\displaystyle U(x_0)\cap E=\varnothing\Rightarrow U(x_0)\subset E^c$, 此时, $x_0$ 为 $\displaystyle E$ 的外点.

---

5、 总结: $\displaystyle x_0$ 与 $\displaystyle E$ 的关系必有且仅有 聚点、孤立点、外点 这三种.

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{c} \mbox{月下独酌四首 $\displaystyle \bullet$ 其一-李白}\\ \mbox{花间一壶酒, 独酌无相亲. } \mbox{举杯邀明月, 对影成三人. }\\ \mbox{月既不解饮, 影徒随我身. } \mbox{暂伴月将影, 行乐须及春. }\\ \mbox{我歌月徘徊, 我舞影零乱. } \mbox{醒时相交欢, 醉后各分散. }\\ \mbox{永结无情游, 相期邈云汉. } \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.3. 边界点要么是聚点, 要么是孤立点

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red} \partial E\subset E'\cup\left\{E \mbox{的孤立点}\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.4. 聚点的等价刻画

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &x_0\mbox{ 是 }E\mbox{ 的聚点}\\ \stackrel{\rm def}{\Leftrightarrow}&(1) \forall\ U(x_0), E\cap U(x_0)\backslash \left\{x_0\right\}\neq \varnothing\\ \Leftrightarrow& (2) \exists\ \mbox{ 互异 }x_n\in E,\mathrm{ s.t.} x_n\to x_0\\ \Leftrightarrow& (3) \forall\ U(x_0),\ U(x_0)\mbox{ 都有 }E\mbox{ 中无限个点}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.5. 闭包的等价刻画

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &(1) x_0\in \bar{E}=E\cup E'\\ \Leftrightarrow& (2) \forall\ U(x_0), \ U(x_0)\cap E\neq \varnothing\quad \left(\mbox{邻域语言刻画}\right)\\ \Leftrightarrow& (3) \exists\ E\ni x_n\to x_0\quad \left(\mbox{序列语言刻画}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注意与导集的等价刻画比较.

02.2.6. 边界与闭包的关系

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \partial E=E^-\cap E^{c-} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.7. 闭包、开核的对偶关系

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E^{-c}&=E^{c\circ},\\ E^{\circ c}&=E^{c-}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

联系 De Morgan 律. $\displaystyle E^\circ \subset E\subset E^-$. $E^\circ$ 比 $\displaystyle E$ 小, 看成交, $\displaystyle E^-$ 比 $\displaystyle E$ 大, 看成并.

02.2.8. 开核, 导集, 闭包保持集合的包含关系

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\subset B\Rightarrow \left\{\begin{array}{llllllllllll} A^\circ\subset B^\circ,\\ A'\subset B',\\ A^-\subset B^-.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.9. 导集与并运算可交换

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (A\cup B)'=A'\cup B'. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

并的导集等于导集的并.

---

2、 思考: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (A\underline{\ \ \ \ \ \ \ \ \ \ } B)^-&=A^-\underline{\ \ \ \ \ \ \ \ \ \ } B^-,\\ (A\underline{\ \ \ \ \ \ \ \ \ \ } B)^\circ&=A^\circ\underline{\ \ \ \ \ \ \ \ \ \ } B^\circ. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.2.10. 导集, 边界不空的充分条件

---

1、 导集不空的一个充分条件 Bolzano-Weierstrass 定理: 设 $\displaystyle E\subset \mathbb{R}^n$ 有界无限, 则 $\displaystyle E'\neq\varnothing$.

---

2、 没见过? 无限集 $A$ 一定有一个可数子集 $\displaystyle \left\{x_n\right\}_{n=1}^\infty$, 而由聚点定理, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ \left\{n_k\right\},\ x_0,\mathrm{ s.t.} \lim_{k\to\infty}x_{n_k}=x_0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这不就找到了 $A$ 中的互异点列 $\displaystyle \left\{x_{n_k}\right\}$ 收敛于 $\displaystyle x_0$, 而 $x_0\in E'$.

---

3、 边界不空的一个充分条件 设 $E\neq \varnothing$, $E\neq \mathbb{R}^n$, 则 $\partial E\neq \varnothing$.

02.3. 开集 (open set), 闭集 (closed set), 完备集 (complete set)

02.3.1. 开集及其性质

---

1、 开区间 $I=(a,b)$ 有啥性质? $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ x\in I,\exists\ \delta=\min\left\{b-x,x-a\right\}\gt 0,\\ &\mathrm{ s.t.} U(x;\delta)\subset I. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这可推广为

---

2、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 是开集}&\stackrel{\rm def}{\Leftrightarrow} E^\circ=E\\ &\Leftrightarrow E\subset E^\circ\\ &\Leftrightarrow \forall\ x_0\in E,\ \exists\ U(x_0)\subset E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\displaystyle E$ 的开核一定是开集 对 $\displaystyle E\subset \mathbb{R}^n$, $E^\circ$ 是开集.

---

4、 开集的性质, 而可构造更多的开集 任意多个开集之并是开集, 有限多个开集之交是开集.

---

5、 反例. 任意多个开集的交不一定是开集. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcap_{n=1}^\infty\left(a-\frac{1}{n},b+\frac{1}{n}\right)=[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.3.2. 闭集及其性质

---

1、

(1)、 闭区间 $\displaystyle [a,b]$,

(2)、 单点集 $\left\{a\right\}=[a,a]$ 是长度退化为 $\displaystyle 0$ 的闭区间.

它们有什么性质? $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red} \mbox{它们的凝聚点还在它们中!}\left\{\begin{array}{llllllllllll} [a,b]'=[a,b],\\ \left\{a\right\}'=\varnothing\subset \left\{a\right\}. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这可推广为

---

2、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 是闭集}&\stackrel{\rm def}{\Leftrightarrow} (1) E'\subset E\\ &\Leftrightarrow (2) E^-=E\\ &\Leftrightarrow (3) \mbox{若 }E\ni x_n\to x_0,\mbox{ 则 }x_0\in E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

由 (3), 我们说 啥是闭集, 就是在极限运算下封闭的集合.

---

3、 对 $\displaystyle E\subset \mathbb{R}^n$, $E^\circ$ 是开集, $\displaystyle E',E^-$ 是闭集.

---

4、 闭集与开集的关系: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{是开集}\Leftrightarrow E^c\mbox{是闭集},\\ E\mbox{是闭集}\Leftrightarrow E^c\mbox{是开集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 闭集的性质, 而可构造更多的闭集 任意多个闭集之交是闭集, 有限多个闭集之并是闭集.

---

6、 任意多个闭集的并不一定是闭集. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \bigcup_{n=1}^\infty\left[a+\frac{1}{n},b-\frac{1}{n}\right]=(a,b). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 正规性: 拓扑的术语 设两闭集 $\displaystyle F_1,F_2$ 不交, 则存在开集 $\displaystyle O_1\supset F_1, O_2\supset F_2$, 使得 $O_1\cap O_2=\varnothing$.

---

8、 思考. 不交闭集的距离一定大于零么?

02.3.4. 紧集、自密集、完备集

---

1、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 是紧集}&\stackrel{\rm def}{\Leftrightarrow} \left(E\subset \bigcup_{\lambda\in \varLambda}O_\lambda\Rightarrow E\subset \bigcup_{i=1}^m O_i\right)\\ &\Leftrightarrow E\mbox{ 是有界闭集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 定义. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 是自密集 (dense-in-itself)} &\stackrel{\rm def}{\Leftrightarrow} E\subset E'\\ &\Leftrightarrow E\mbox{ 没有孤立点}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{是完备集 (complete set)}&\stackrel{\rm def}{\Leftrightarrow} E=E'\\ &\Leftrightarrow E\mbox{是自密闭集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. $\varnothing$ 是自密集, 也是完备集.

---

5、 例. 在 $\displaystyle \mathbb{R}$ 中, $\displaystyle \mathbb{Q}$ 是自密集, $\displaystyle [a,b]$ 和 $\displaystyle \mathbb{R}$ 是完备集.

---

6、 总结. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{是闭集}&\Leftrightarrow E'\subset E,\\ E\mbox{是自密集}&\Leftrightarrow E\subset E',\\ E\mbox{是完备集}&\Leftrightarrow E'=E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.4. 直线上的开集、闭集及完备集的构造

02.4.1. 直线上的开集、闭集的构造

---

1、 直线上的开集的构造: 直线上的开集 $\displaystyle O$ 是至多可数个互不相交的开区间的并, 也即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &O=\bigcup_{k=1}^{m\mbox{ 或 }\infty}(a_k,b_k),\\ &k\neq l\Rightarrow (a_k,b_k)\cap (a_l,b_l)=\varnothing. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 直线上闭集的构造. 对闭集 $\displaystyle F\subset \mathbb{R}$, $F^c$ 是开集, 而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} F^c=\bigcup_{k=1}^{m\mbox{ 或 }\infty} (a_k,b_k). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称 $\displaystyle (a_k,b_k)$ 为 $\displaystyle F$ 的余区间或邻接区间.

02.4.2. 直线上完备集的构造

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} F(\subset \mathbb{R})\mbox{ 是完备集}&\Leftrightarrow F\mbox{ 是自密闭集}\\ &\Leftrightarrow F\mbox{ 是没有孤立点的闭集}\\ &\Leftrightarrow F\mbox{ 的邻接区间没有公共端点}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.5. Cantor 三分集 (Cantor third-middle set)

02.5.1. Cantor 三分集的构造

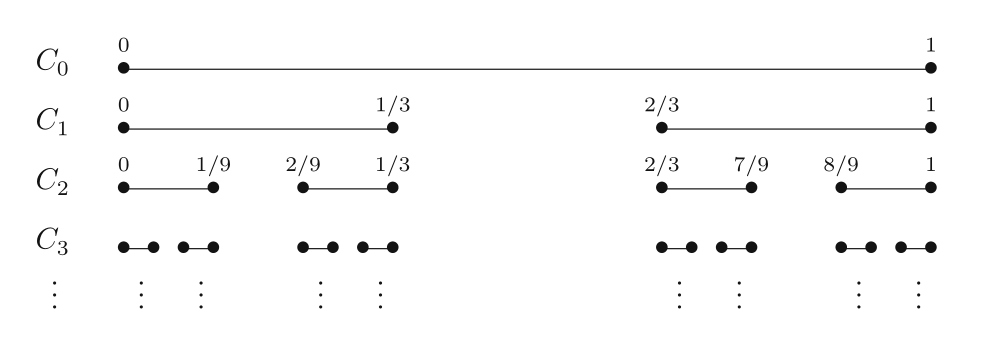
把 $\displaystyle [0,1]$ 三等分, 挖去中间的那段, 记剩下的 $\displaystyle 2$ 个区间的并为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{$F_1$ (由$2$ 个长度为 $\displaystyle 1/3$ 的闭区间组成).} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

若 $\displaystyle F_{n-1}$ 已给出, 则对其 $\displaystyle 2^{n-1}$ 个闭区间三等分, 挖去中间的那段, 记剩下的 $\displaystyle 2^n$ 个区间的并为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{$F_n$ (由$2^n$ 个长度为 $\displaystyle 1/3^n$ 的闭区间组成).} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

一直做下去, 得到一个递减闭集列 $\displaystyle \left\{F_n\right\}_{n=1}^\infty$. 定义: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{Cantor 三分集 } P \stackrel{\rm def}{=}&\bigcap_{n=1}^\infty F_n\\ =&\lim_{n\to\infty}F_n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

02.5.2. Cantor 三分集的性质

---

1、 $P$ 是完备集.

---

2、 $\displaystyle P$ 没有内点 (而是疏朗集 nowhere dense set).

---

3、 $\displaystyle [0,1]\backslash P$ 是可数个互不相交的开区间的并, 总长为 $\displaystyle 1\Rightarrow P$ 的 测度为 $\displaystyle 0$.

---

4、 $P$ 的基数为 $\displaystyle c$.

---

5、 总结: Cantor 三分集是一个测度为零且基数为 $c$ 的疏朗完备集.

02.5.3. 维数观点看 Cantor 集

用测度 (或长度) 来考查 Cantor 集貌似不对. 因为长度为零在我们的直观中就是一点. 基数怎么会为 $\displaystyle c$ 呢? 元素的个数比自然数集还多呢. 换个方向考虑, 就是维数 (dimension).

Cantor 集的维数为 $\displaystyle \mathrm{log}_3 2\approx 0.631$, 分数维! 感兴趣可以去学分形几何的啦.

02.6. 本章小结

---

1、 度量空间.

---

2、 点与集合的关系

(1)、 内点, 外点, 界点 (内点全体 $E^\circ$, 外点全体 $E^{c\circ}$, 界点全体 $\partial E$).

(2)、 聚点, 孤立点, 外点 (聚点全体 $E'$, 外点全体 $E^{c\circ}$).

(3)、 聚点的刻画, 闭包的刻画.

(4)、 对偶律: $E^{-c}=E^{c\circ}$, $E^{\circ c}=E^{c-}$ (和 De Morgan 律比较)

(5)、 导集不空的条件, 边界不空的条件.

---

3、 开集, 闭集, 紧集, 自密集, 完备集的概念, 性质, 例子

(1)、 对偶律: $\displaystyle E$ 是开集 $\displaystyle \Leftrightarrow E^c$ 是闭集.

---

4、 直线上开集, 闭集, 完备集的构造.

---

5、 Cantor 三分集的构造及其性质.

03. 测度论 (measurable set

03.0. 引言

---

1、 我们的经验是长度公理: 对直线上的一些点集构成的集族, 指定其上的一个函数 $\displaystyle m$, 使得

(1)、 非负性 (non-negativity): $mE\gt 0$;

(2)、 有限可加性 (finitely additivity): 若 $\left\{E_i\right\}_{i=1}^j$ 互不相交, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} m(E_1\cup \cdots\cup E_j)=mE_1+\cdots+mE_j; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 正则性 (unity): $\displaystyle m([0,1])=1$.

---

2、 Lebesgue (为了使更多的集合可求长度, 而使得更多的函数可积分) 将其推广为

(1)、 非负性 (non-negativity): $mE\gt 0$;

(2)、 可数可加性 (countably additivity): 若 $\left\{E_i\right\}_{i=1}^\infty$ 互不相交, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} m\left(\bigcup_{i=1}^\infty E_i\right) =\sum_{i=1}^\infty mE_i; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 正则性 (unity): $\displaystyle m([0,1])=1$.

这就是我们本章要学习的 测度.

03.1. 外测度 (outer measure)

---

1、 原始的想法: 用规则的可求测度的集合 (比如区间) 去逼近任一集合 $E$. 若 外包 的下确界 $=$ 内测度 内填 的上确界, 则 $\displaystyle E$ 是可测的.

---

2、 但是这样就涉及到两个概念: 外测度, 内测度. 现代书一般就给出外测度, 然后加上一个条件 (Caratheodory 条件), 使得其与 外测度 $\displaystyle =$ 内测度 等价. 这样就不用引进内测度了.

---

3、 对 $\displaystyle E\subset \mathbb{R}^n$, 定义 $E$ 的外测度 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} m^\star E=\inf\left\{\sum_{n=1}^\infty |I_i|; E\subset \bigcup_{n=1}^\infty I_i\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是用可数个开区间去盖 $\displaystyle E$.

---

4、 外测度的性质:

(1)、 $m^\star E\gt 0$, $m^\star \varnothing=0$.

(2)、 单调性 (monotonicity) $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\subset B\Rightarrow m^\star A\leq m^\star B. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 次可数可加性 (sub countably additivity): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} m^\star \left(\bigcup_{n=1}^\infty A_i\right)\leq \sum_{n=1}^\infty m^\star A_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 例. 对任何区间 $I$, 有 $m^\star I=|I|$.

---

6、 例. $\mathbb{R}^n$ 中的单点集 $\displaystyle \left\{x_0\right\}$ 满足 $\displaystyle m^\star \left\{x_0\right\}=0$.

---

7、 例. $m^\star \mathbb{Q}=0$.

03.2. 可测集 (measurable set)

03.2.1. 可测集的等价定义

---

1、 $\mathbb{R}^n$ 中集合 $\displaystyle E$ 称为可测的 (measurable), 如果

$$\begin{equation}\tag{3.2: Caratheodory}\label{3.2: Caratheodory}\begin{aligned} m^\star T=m^\star (T\cap E)+m^\star (T\cap E^c),\\ \forall\ T\subset \mathbb{R}^n. \end{aligned}\end{equation}$$

$\displaystyle E$ 可测当且仅当上述试验对所有 $\displaystyle \mathbb{R}^n$ 的子集都成立. 这里只涉及到外测度, 而不用引入内测度了.

(1)、 所有可测集构成的集族记为 $\displaystyle \mathfrak{M}$.

(2)、 这里的 $T$ 称为试验集 (test set).

(3)、 \eqref{3.2: Caratheodory} 称为 Caratheodory 条件.

(4)、 当 $\displaystyle E\in \mathfrak{M}$ 时, 记 $\displaystyle mE$ 为 $\displaystyle E$ 的测度: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} mE=m^\star E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 可不可测, 只需对所有区间做试验即可. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &E\in\mathfrak{M}\\ \stackrel{\rm def}{\Leftrightarrow}&m^\star T=m^\star (T\cap E)+m^\star (T\cap E^c),\ \forall\ T\subset \mathbb{R}^n\\ \Leftrightarrow&m^\star I=m^\star (I\cap E)+m^\star (I\cap E^c),\ \forall\ I\subset \mathbb{R}^n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 可不可测只需看它是否在外测度意义下分离集合.

$$\begin{equation}\tag{3.2: measure-property-separation}\label{3.2: measure-property-separation}\begin{aligned} &E\in\mathfrak{M}\\ \stackrel{\rm def}{\Leftrightarrow}& m^\star T=m^\star (T\cap E)+m^\star (T\cap E^c),\\ &\forall\ T\subset \mathbb{R}^n\\ \Leftrightarrow& m^\star (A\cup B)=m^\star A+m^\star B,\\ &\forall\ A\subset E, B\subset E^c. \end{aligned}\end{equation}$$

03.2.2. 可测集的性质1: 可测集的补, 可测集列的交与并

---

1、 可测集类对补运算封闭. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\in\mathfrak{M}\Rightarrow E^c\in\mathfrak{M}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 可测集类对交/并运算封闭. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E_1,E_2\in\mathfrak{M}\Rightarrow \left\{\begin{array}{llllllllllll} E_1\cup E_2\in \mathfrak{M}\\ E_1\cap E_2\in\mathfrak{M}\end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 可测集类对有限交/有限并运算封闭. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{E_i\right\} _{i=1}^n\subset\mathfrak{M} \Rightarrow\left\{\begin{array}{llllllllllll} \bigcup_{i=1}^n E_i\in\mathfrak{M}\\ \bigcap_{i=1}^n E_i\in\mathfrak{M}\end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 可测集类对可数并运算封闭, 且有 可数可加性 countable additivity. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{E_i\right\}_{i=1}^\infty\subset\mathfrak{M}\Rightarrow \bigcup_{i=1}^\infty E_i\in\mathfrak{M}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

且

$$\begin{equation}\tag{3.2: measure-property-countably-additivity}\label{3.2: measure-property-countably-additivity}\begin{aligned} &\left\{\begin{array}{llllllllllll}E_i\in \mathfrak{M}\\ E_i\cap E_j=\varnothing\ (i\neq j)\end{array}\right.\\ \Rightarrow& m\left(\bigcup_{i=1}^\infty E_i\right)=\sum_{i=1}^\infty mE_i. \end{aligned}\end{equation}$$

---

5、 可测集类对可数交运算封闭. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{E_i\right\} _{i=1}^\infty\subset\mathfrak{M}\Rightarrow \bigcap_{i=1}^\infty E_i\in\mathfrak{M}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

03.2.3. 可测集的性质2: 可测集列的极限

---

1、 测度与递增极限运算可交换. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathfrak{M}\supset \left\{E_i\right\}\nearrow \Rightarrow m\left(\lim_{i\to\infty}E_i\right)=\lim_{i\to\infty}mE_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 在测度有限时, 测度与递减极限运算可交换. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{rrrr}\mathfrak{M}\supset \left\{E_i\right\}\searrow\\ mE_1\lt \infty \end{array}\right\}\Rightarrow m\left(\lim_{i\to\infty} E_i\right)=\lim_{i\to\infty}mE_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 反例. 在测度无限时, 测度与递减极限运算不一定可交换哦.

03.3. 可测集类

03.3.1. 可测集的例子

---

1、 零测度集可测: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 是零测度集}\stackrel{\rm def}{\Leftrightarrow} m^\star E=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 (开、闭、半开半闭) 区间 $\displaystyle I$ 可测, 且 $\displaystyle mI=|I|$.

---

3、 开集、闭集可测.

---

4、 Borel 集可测.

(1)、 $\sigma$ 代数: 就是一个集族 $\displaystyle \varOmega$, 其满足

(1-1)、 $\mathbb{R}^n \in \varOmega$,

(1-2)、 $\varOmega$ 对可数并运算封闭: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{A_i\right\}_{i=1}^\infty \subset \varOmega \Rightarrow \bigcup_{i=1}^\infty A_i\in \varOmega, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(1-3)、 $\displaystyle \varOmega$ 对补运算封闭: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\in \varOmega\Rightarrow A^c\in \varOmega. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 当然, 随便给一个集族 $\displaystyle \varSigma$, 其不一定是 $\sigma$ 代数. 但是我们可以考虑 由 $\displaystyle \varSigma$ 生成的 $\displaystyle \sigma$ 代数 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \sigma(\varSigma)=\bigcap_{\varOmega\supset \varSigma}\varOmega. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是啥? 就是把包含 $\displaystyle \varSigma$ 的所有 $\displaystyle \sigma$ 代数交起来; 换句话说, 是包含 $\displaystyle \varSigma$ 的最小 $\displaystyle \sigma$ 代数. 比较线性包, 凸包.

(3)、 Borel 代数: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{由 }\mathbb{R}^n\mbox{ 中所有开集生成的 }\sigma\mbox{ 代数, 记作 }\mathfrak{B}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(4)、 Borel集: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{集族} \mathfrak{B}\mbox{ 中的集合}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

03.3.2. 可测集的构造

---

1、 定义: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} G_\delta\mbox{ 集}: & G=\bigcap_{i=1}^\infty O_i\left(\mbox{可数个开集的交}\right)\\ F_\sigma\mbox{ 集}: & F=\bigcup_{i=1}^\infty F_i\left(\mbox{可数个闭集的并}\right). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们已经知道有限个开集的交是开集, 但可数个开集的交就不一定是开集的嘛. 所以我们给出上述定义.

---

2、 正如开集与闭集对偶一样, $\displaystyle G_\delta$ 集与 $\displaystyle F_\sigma$ 集对偶.

---

3、 可测集长啥样? 嘿. 可测集 $\displaystyle = G_\delta$ 集 $\displaystyle \backslash$ 零测度集: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 可测}\Rightarrow& \exists\ G_\delta\mbox{ 集 }G,\mbox{ 零测度集 }Z_1,\\ &\mathrm{ s.t.} E=G\backslash Z_1. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 可测集 $\displaystyle = F_\sigma$ 集 $\displaystyle \cup$ 零测度集: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E\mbox{ 可测}\Rightarrow& \exists\ F_\sigma\mbox{ 集}, \mbox{零测度集 }Z_2,\\ &\mathrm{ s.t.} E=F\cup Z_2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

03.3.3. 测度的内、外正规性

---

1、 可测集的测度可用开集/紧集的测度来逼近. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &E\mbox{ 可测}\\ \Rightarrow&\left\{\begin{array}{ll} (\mbox{外正规性}): mE=\inf \left\{mO;\ O\supset E\right\}\\ (\mbox{内正规性}): mE=\sup\left\{mK; K\subset E\right\} \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

外包/内填嘛. 外可用开集的测度逼近/内可用紧集的测度逼近.

03.4. 本章小结

---

1、 外测度及其三条性质.

---

2、 可测集及其性质 (最重要的: 对可数并, 可数交, 补封闭; 单增可测集列极限与测度可交换; 测度有限时, 单减可测集列极限与测度可交换).

---

3、 可测集的例子 (零测度集, 区间, 开集, 闭集, Borel 集).

---

4、 可测集的构造 ($G_\delta\backslash Z_1$, $\displaystyle F_\sigma\cup Z_2$).

---

5、 测度的内外正规性.

04. 可测函数 (measurable function)

04.0. 引言

---

1、 Riemann 积分主要考虑连续函数: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\in C(\mathbb{R}^n)\\ \Leftrightarrow&\forall\ c\in\mathbb{R},\ \begin{array}{c}\left\{x;f(x)\lt c\right\}\\ \left\{x;f(x)\gt c\right\}\end{array}\mbox{ 都是开集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Lebesgue 想考虑更为广泛的函数 (使其可积分): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\mbox{ 是 }E\mbox{ 上的可测函数}\\ \Leftrightarrow& \forall\ c\in \mathbb{R},\ \left\{x;f(x)\lt c\right\}\mbox{ 是可测集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这就是本章要学习的 可测函数.

04.1. 可测函数 (measurable function) 及其性质

04.1.1. 记号 (notations)

---

1、 广义实数: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\mathbb{R}}=\mathbb{R}\bigcup\left\{-\infty\right\}\bigcup\left\{+\infty\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 本章主要考虑 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f: E\to \overline{\mathbb{R}}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

其中 $E$ 是可测集, 而把 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f: E\to \mathbb{R} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 有限函数.

---

3、 有限函数、有界函数的区别.

(1)、 有限函数不一定有界, 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\frac{1}{x},\ x\in (0,1]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 有界函数一定有限.

---

4、 $\displaystyle x$ 是哑巴, 可以去掉, 也可以换成其它符号. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E[f\gt c]=\left\{x\in E;f(x)\gt c\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

和定积分的积分变量类比.

04.1.2. 可测函数的定义及等价刻画

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f: E\to \overline{\mathbb{R}}\mbox{ 是可测函数}\\ \stackrel{\rm def}{\Leftrightarrow}& \forall\ c\in\mathbb{R}, E[f\gt c]\mbox{ 是可测集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D(x)=\left\{\begin{array}{llllllllllll} 1,&x\in \mathbb{Q}\\ 0,&x\in \mathbb{R}\backslash\mathbb{Q} \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

可测.

---

3、 例. $\displaystyle E=(a,b)$ 上的单调函数可测.

---

4、 可测函数的等价定义: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &($\star$) f\mbox{ 可测}\stackrel{\rm def}{\Leftrightarrow}\forall\ c\in\mathbb{R}, E[f\gt c]\mbox{ 是可测集}\\ \Leftrightarrow &(1) \forall\ c\in\mathbb{R}, E[f\gt c]\mbox{ 可测},\\ \Leftrightarrow &(2) \forall\ c\in\mathbb{R}, E[f\lt c] \mbox{ 可测},\\ \Leftrightarrow &(3) \forall\ c\in\mathbb{R}, E[f\leq c]\mbox{ 可测},\\ \Leftrightarrow &(4) \forall\ a,b\in\mathbb{R},\ a\lt b, E[a\leq f\lt b]\mbox{ 可测},\\ &(\Leftarrow\mbox{ 需要 }f \mbox{ 是有限函数}). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 函数可测的必要条件, 非充分哦. 如果 $\displaystyle f: E\to \bar{\mathbb{R}}$ 可测, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ c\in\bar{\mathbb{R}}, E[f=c]\mbox{可测}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.1.3. 重要的可测函数类 I---连续函数类

---

1、 设 $\displaystyle f: E\to \overline{\mathbb{R}}$, 如果 $f(x_0)\in\mathbb{R}$, 且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\mathrm{ s.t.}\\ &x\in E\cap U(x_0;\delta) \Rightarrow |f(x)-f(x_0)|\lt \varepsilon, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $f$ 在点 $\displaystyle x_0$ 处连续.

---

2、 $\displaystyle f$ 在 $\displaystyle E$ 的孤立点上连续.

---

3、 可测集上的连续函数必可测 设 $\displaystyle f: E\to\overline{\mathbb{R}}$ 连续, 则 $\displaystyle f$ 可测.

04.1.4. 重要的可测函数类 II---简单函数类

---

1、 可测函数在可测子集上还可测. 设 $\displaystyle f$ 在 $\displaystyle E$ 上可测, $\displaystyle \tilde{E}(\subset E)$ 可测, 则 $\displaystyle f$ 在 $\displaystyle \tilde{E}$ 上的限制 $\displaystyle f: \tilde{E}\to\overline{\mathbb{R}}$ 也可测.

---

2、 至多可数个可测集上的可测函数可测. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mbox{$f$ 在$\left\{E_i\right\}_{i=1}^{j\mbox{ 或 }+\infty}$ 上可测}\\ \Leftrightarrow&\mbox{$f$ 在 $\displaystyle E=\bigcup_{i=1}^{j\mbox{ 或 }+\infty}E_i$ 上可测.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 定义. 设 $\displaystyle \left\{E_i\right\}_{i=1}^j$ 两两不交, 可测, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f: E=\bigcup_{i=1}^j E_i\to \overline{\mathbb{R}} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=c_i, x\in E_i, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle f$ 为 简单函数 simple function, 记作 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\sum_{i=1}^j c_i\chi_{E_i}(x),\quad x\in E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这里及以后用 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \chi_A(x)=\left\{\begin{array}{llllllllllll} 1,&x\in A\\ 0,&x\not\in A \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

表示集合 $\displaystyle A$ 的特征函数 (characteristic function).

---

4、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D(x)=\left\{\begin{array}{llllllllllll} 1,&x\in \mathbb{Q}\\ 0,&x\in \mathbb{R}\backslash\mathbb{Q} \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是 $\displaystyle \mathbb{R}$ 上的简单函数.

---

5、 简单函数可测.

04.1.5. 可测函数的四则运算

---

1、 只要有意义, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f,g\mbox{可测}\Rightarrow f\pm g, f\cdot g, \frac{f}{g}\mbox{可测}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\mbox{ 可测}\Leftrightarrow \left\{\begin{array}{llllllllllll} \mbox{正部 }f^+\stackrel{\rm def}{=}\max\left\{f,0\right\}\gt 0\\ \mbox{负部 }f^-\stackrel{\rm def}{=}-\min\left\{f,0\right\}\gt 0 \end{array}\right. \mbox{ 可测}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.1.6. 可测函数的极限运算

---

1、 思考. 四则运算和绝对值运算是连续函数所保持的. 那你看看如下的极限运算连续函数还保持么? 也即: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f_n\in C[a,b]; \lim_{n\to\infty}f_n(x)=f(x)\\ \Rightarrow& (?) f\in C[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 哇瑟. 极限运算为可测函数所保持. 先看上下确界的情形. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_i\mbox{ 可测}\Rightarrow \left\{\begin{array}{llllllllllll} m(x)=\inf_{i\gt 1}f_i(x)\mbox{ 可测},\\ M(x)=\sup_{i\gt 1}f_i(x)\mbox{ 可测}.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 再看上下极限的情形. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_i\mbox{ 可测}\Rightarrow \left\{\begin{array}{llllllllllll} \varliminf_{i\to\infty}f_i\mbox{ 可测},\\\varlimsup_{i\to\infty}f_i\mbox{ 可测}.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 极限运算自然不在话下.

04.1.7. 可测函数与简单函数的关系

---

1、 非负可测函数可以通过简单函数递增逼近. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\mbox{ 非负可测}\\ \Rightarrow& \exists\mbox{ 简单函数列 }\left\{\phi_k\right\},\mathrm{ s.t.} \phi_k\nearrow f. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 一般可测函数可以通过简单函数逐点逼近. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\mbox{ 可测}\Rightarrow \exists\ \mbox{ 简单函数列 }\phi_k,\mathrm{ s.t.} \phi_k\to f. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 有界可测函数可以通过简单函数一致逼近. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\mbox{ 有界可测}\Rightarrow \exists\mbox{ 简单函数列 }\left\{\phi_k\right\},\mathrm{ s.t.} \phi_k\rightrightarrows f. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 总结: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{ 非负可测}&\Rightarrow\mbox{递增逼近},\\ \mbox{可测}&\Rightarrow \mbox{点点逼近},\\ \mbox{有界可测}&\Rightarrow \mbox{一致逼近}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.1.8. 几乎处处成立的内涵

---

1、 设 $\displaystyle E$ 是集合, $\displaystyle \pi(x)$ 是与 $\displaystyle x$ 有关的命题, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ Z\subset E,\ mZ=0,\mathrm{ s.t.} \pi(x)\mbox{ 在 }E\backslash Z\mbox{ 上成立}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle \pi$ 在 $\displaystyle E$ 上几乎处处成立, 记作 $\displaystyle \pi\ \mbox{a.e.}$ 于 $\displaystyle E$ (almost everywhere). $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\pi(x) \mbox{a.e.} \mbox{于} E\\ \Leftrightarrow& m\left\{x\in E; \pi(x)\mbox{ 不成立}\right\}=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例 1.$\tan x$ 在 $\displaystyle \mathbb{R}$ 上几乎处处有限.

---

3、 例 2. Dirichlet 函数 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D(x)=\left\{\begin{array}{llllllllllll} 1,&x\in \mathbb{Q}\\ 0,&x\in \mathbb{R}\backslash\mathbb{Q}\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

几乎处处为零.

---

4、 例 3. $\displaystyle \sin x$ 几乎处处小于 $\displaystyle 1$.

---

5、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{ll} \pi_1,\mbox{a.e.}\mbox{ 于 }E\\ \pi_2,\mbox{a.e.}\mbox{ 于 }E \end{array}\right\}\Rightarrow \pi_1\mbox{ 且 } \pi_2,\mbox{a.e.}\mbox{ 于 }E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{ll} f=g,\mbox{a.e.}\mbox{ 于 }E\\ g=h,\mbox{a.e.}\mbox{ 于 }E \end{array}\right\}\Rightarrow f=h,\mbox{a.e.}\mbox{ 于 }E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.2. Egrov 定理

04.2.1. 引言

---

1、 一致收敛很重要. 比如可以用于极限与积分交换次序等.

---

2、 可惜的是很多时候不一致收敛. 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k(x)=x^k\to f(x)=\left\{\begin{array}{ll} 0,&x\in [0,1)\\ 1,&x=1 \end{array}\right.,\ x\in [0,1]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

因为极限函数不连续.

---

3、 但 $\forall\ 0\lt \delta\lt 1$, $f_k$ 在 $\displaystyle [0,1-\delta]$ 上一致收敛! 除掉一个长度可以任意小的集合 $\displaystyle (1-\delta,1]$ 之外是一致收敛的.

---

4、 本节的内容就是把这种现象普适化.

04.2.2. Egrov 定理

---

1、 Egrov 定理 设

(1)、 $\displaystyle mE\lt \infty$;

(2)、 $\mbox{a.e.}$ 有限的可测函数列 $\displaystyle \left\{f_k\right\}$ $\mbox{a.e.}$ 收敛于 $\displaystyle \mbox{a.e.}$ 有限的函数 $\displaystyle f$.

则 $f_k$ 在 $\displaystyle E$ 上基本上一致收敛于 $\displaystyle f$: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \delta\gt 0,\ \exists\ E_\delta\subset E,\ mE_\delta\lt \delta,\mathrm{ s.t.}\\ &f_k\rightrightarrows f\mbox{ 于 }E\backslash E_\delta\mbox{ 上}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Egrov 定理的意义: 在测度有限的可测集上, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{a.e.}\mbox{ 收敛}\Rightarrow \mbox{基本上一致收敛}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 反例. $mE=+\infty$ 时, Egrov 定理不一定不成立. 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k(x)=\chi_{[k,k+1]}(x),\quad x\in \mathbb{R}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 Egrov 定理的逆定理在 $\displaystyle mE\leq+\infty$ 时成立. 做作业吧. 哈哈.

04.2.3. Egrov 定理的推广

---

1、 Egrov 定理的推广 设

(1)、 $\displaystyle mE\lt +\infty$;

(2)、 $\mbox{a.e.}$ 有限的可测函数列 $\displaystyle \left\{f_k\right\}$ $\mbox{a.e.}$ 发散于 $\displaystyle +\infty$.

则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \delta\gt 0, \exists\ E_\delta\subset E, mE_\delta\lt \delta,\mathrm{ s.t.}\\ &f_k\rightrightarrows +\infty,\mbox{ 于 }E\backslash E_\delta\mbox{ 上}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.3. 可测函数的构造

04.3.1. Lusin 定理

---

1、 Lusin 定理 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\mbox{ 是可测集 }E\mbox{ 上 }\mbox{a.e.} \mbox{ 有限的可测函数}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $f$ 基本上连续: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \delta\gt 0,\ \exists\ \mbox{ 闭集 }F_\delta\subset E,\ m(E\backslash F_\delta)\lt \delta,\\ &\mathrm{ s.t.} f\mbox{ 在 }F_\delta\mbox{ 上连续}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Lusin 定理的意义: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{可测函数基本上连续}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.3.2. Lusin 定理的另一形式

---

1、 Lusin 定理的另一形式: 设 $\displaystyle f$ 是 $\displaystyle E\subset\mathbb{R}$ 上 $\displaystyle \mbox{a.e.}$ 有限的可测函数, 则 (注意几何意义) $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \delta\gt 0,\ \exists\ F\subset E: m(E\backslash F)\lt \delta, g\in C(\mathbb{R}), \mathrm{ s.t.} \\ &g|_F=f,\ \sup_{\mathbb{R}}g=\sup_Ff,\ \inf_{\mathbb{R}}g=\inf_Ff. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.3.3. 可测集与可测函数的总结

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{lll} &\mbox{集 $\displaystyle E$ 可测}&\mbox{函数 $\displaystyle f: E\to \bar{\mathbb{R}}$ 可测}\\ \hline \boxed{\begin{array}{c}\mbox{定}\\ \mbox{义}\end{array}}& \boxed{\begin{array}{l} m^\star T\\ =m^\star (T\cap E)\\ +m^\star (T\cap E^c),\\ \forall\ T\subset \mathbb{R}^n\end{array}} &\boxed{\begin{array}{r} \mbox{$E[f\gt c]$ 可测},\\ \forall\ c\in\mathbb{R}\end{array}}\\ \hline \boxed{\begin{array}{c}\\ \mbox{刻}\\ \mbox{画}\end{array}}& \boxed{\begin{array}{c}\mbox{只要对区间做}\\ \mbox{试验, 在外测度}\\ \mbox{意义下分离集合}\end{array}}&\boxed{\begin{array}{c}\mbox{$\gt$ 可改成任一}\\ \mbox{(严格) 不等号: }\\ \gt, \lt , \leq\end{array}}\\ \hline \boxed{\begin{array}{c}\mbox{性}\\ \mbox{质}\end{array}}&\boxed{\begin{array}{c}\mbox{对补, 可数交,}\\ \mbox{可数并封闭}\end{array}}&\boxed{\begin{array}{c}\mbox{四则运算}\\ \mbox{极限运算}\end{array}}\\ \hline \boxed{\begin{array}{c}\mbox{例}\\ \mbox{子}\end{array}}&\boxed{\begin{array}{c}\mbox{零测度集, 区间,}\\ \mbox{开集, 闭集,}\\ \mbox{$F_\sigma$ 集, $\displaystyle G_\delta$ 集,}\\ \mbox{Borel 集}\end{array}} &\boxed{\begin{array}{c}\mbox{Dirichlet 函数,}\\ \mbox{单调函数,}\\ \mbox{连续函数,}\\ \mbox{简单函数}\end{array}}\\ \hline \boxed{\begin{array}{c}\mbox{构}\\ \mbox{造}\end{array}}&\boxed{\begin{array}{rr}E=&G_\delta\backslash Z_1\\ =&F_\sigma\cup Z_2\end{array}}&\boxed{\begin{array}{l}\mbox{可测函数基本上连续;}\\ \mbox{非负可测由简单函数递增逼近,}\\ \mbox{可测由简单函数逐点逼近,}\\ \mbox{有界可测由简单函数一致逼近}\end{array}}\\ \hline \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4. 依测度收敛 (convergence in measure)

04.4.1. 依测度收敛的定义

---

1、 以前学过 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{点态收敛},\quad \mbox{一致收敛}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

本节将用测度引进另外一种收敛概念---依测度收敛: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ (f_k\Rightarrow f)\ (\mbox{菲赫金哥尔茨的记号})\\ &\stackrel{\rm def}{\Leftrightarrow} \forall\mbox{ 误差 }\sigma\gt 0,\ E[|f_k-f|\gt \sigma]\mbox{ 虽然可能很多},\\ &\quad \ \mbox{ 但其测度 }\to 0\ (k\to\infty). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 依测度收敛: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (f_k\Rightarrow f)\stackrel{\rm def}{\Leftrightarrow} \forall\ \sigma\gt 0,\ \lim_{k\to\infty}m [|f_k-f|\gt \sigma]=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.2. 依测度收敛不能蕴含几乎处处收敛

---

1、 依测度收敛但不收敛的例子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_{k,j}(x)= \chi_{\left(\frac{j-1}{2^k},\frac{j}{2^k}\right]}(x),\ j=1,2,\cdots,2^k. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.3. 几乎处处收敛不能蕴含依测度收敛

---

1、 $\displaystyle \mbox{a.e.}$ 收敛但不依测度收敛的例子. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k(x)=\left\{\begin{array}{ll} 0,&x\in (0,k]\\ 1,&x\in (k,+\infty) \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.4. Riesz 定理 (依测度收敛函数列有一个子列几乎处处收敛)

---

1、 Riesz 定理 依测度收敛函数列有一个子列几乎处处收敛. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (f_k\Rightarrow f)\Rightarrow \exists\ \left\{k_j\right\},\mathrm{ s.t.} f_{k_j}\to f, \mbox{a.e.}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.5. Lebesgue 定理 (测度有限时, 几乎处处收敛蕴含依测度收敛)

---

1、 Lebesgue 设 $\displaystyle mE\lt \infty$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mbox{a.e.}\mbox{有限的可测函数列 }f_k\mbox{a.e.} \mbox{收敛于 }\\ &\mbox{a.e.}\mbox{有限的函数}f. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $f_k\Rightarrow f$.

---

2、 反例. Lebesgue 定理中 $mE\lt \infty$ 是必须的. 否则有反例 没错. 就是刚刚学的那个几乎处处收敛不能蕴含依测度收敛的例子: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k(x)=\left\{\begin{array}{ll} 0,&x\in (0,k]\\ 1,&x\in (k,+\infty) \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.6. 依测度收敛的极限的唯一性 (在几乎处处意义下)

---

1、 依测度收敛的极限的唯一性 (在 $\displaystyle \mbox{a.e.}$ 意义下). $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{rrrr} f_k\Rightarrow f\\ f_k\Rightarrow g \end{array}\right\} \Rightarrow f=g,\mbox{a.e.}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.7. 各种收敛态的关系总结

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{ccccc} &\small\begin{array}{c}\mbox{Egrov,}\\mE\lt \infty, \mbox{基本上}\end{array}&&\small\mbox{Riesz, 子列}\\ \left[f_k\rightrightarrows f\right] &\leftrightarrows& \left[f_k\to f\mbox{a.e.}\right] &\leftrightarrows& \left[f_k\Rightarrow f\right]\\ &\small\mbox{无条件}&&\small\begin{array}{c}\mbox{Lebesgue,}\\mE\lt \infty\end{array} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

04.4.8. Riesz 定理的强化版本

---

1、 Riesz 定理的强化版本 直接建立依测度收敛与一致收敛的关系. 设 $\displaystyle E\subset \mathbb{R}^n$ 是可测集, $\displaystyle f_k,f$ 均是 $\displaystyle E$ 上的 $\displaystyle \mbox{a.e.}$ 有限的可测函数. 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k\Rightarrow f, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle \exists\ \left\{k_i\right\},\mathrm{ s.t.} f_{k_i}$ 基本上一致收敛于 $\displaystyle f$.

04.5. 本章小结

---

1、 可测函数的等价定义, 四则运算, 上极限/下极限/极限运算.

---

2、 重要的可测函数类

(1)、 连续函数类, 及其与可测函数的关系: Lusin 定理.

(2)、 重要的可测函数类: 简单函数类. 其与可测函数的关系: 非负可测时, 递增逼近; 有界可测时, 一致逼近; 一般可测时, 点点逼近.

---

3、 可测函数列各种收敛及其关系: 一致收敛, 几乎处处收敛, 依测度收敛.

05. 积分论 (theory of integration)

05.1. Riemann 积分的局限性, Lebesgue 积分简介

05.1.1. Riemann 积分的局限性

---

1、 Riemann 积分与极限的条件太严: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_k\rightrightarrows f\Rightarrow \lim \int_a^b f_k =\int_a^b \lim f_k. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这 一致收敛 极大地限制了 Riemann 积分的应用.

---

2、 积分运算不完全是微分运算的逆运算: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\mbox{ 在 }x\mbox{ 连续}\Rightarrow \frac{\mathrm{ d}}{\mathrm{ d} x}\int_a^x f(t)\mathrm{ d} t=f(x), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

但微分后再积分不一定能还原. 比如 Volterra 于 1881 年构造了一可微函数 $F(x)$, 其导函数 $f(x)$ 有界但不 Riemann 可积, 而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} F(x)=F(a)+\int_a^xf(t)\mathrm{ d} t \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

不成立.

05.1.2. Lebesgue 积分简介

---

1、 鉴于 Riemann 积分的以上缺陷, Lebesgue 于 1902 年引入了 Lebesgue 积分, 很大程度上摆脱了以上 Riemann 积分的困境.

---

2、 Lebesgue 积分的的步骤

(1)、 Riemann 积分主要为: 竖分割, 求和, 取极限: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim \sum f(\xi_i)\cdot (x_i-x_{i-1}); \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 Lebesgue 积分主要为: 横分割, 求和, 取极限: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim \sum y_i\cdot mE[y_i\leq f\lt y_{i+1}]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Lebesgue 积分的基本思路

(1)、 易知 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\gt 0\Rightarrow&\mbox{积分 $\displaystyle \gt 0$;}\\ f\leq 0\Rightarrow&\mbox{积分 $\leq 0$;}\\ \mbox{一般}f\Rightarrow&\mbox{ 积分 $=$ 正、负面积的代数和.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们考虑的可测函数 $\displaystyle f: E\to\overline{\mathbb{R}}$, 其正面积可能为 $\infty$, 负面积可能为 $\infty$, 而可能出现 $\infty-\infty$ 的不定情形. 所以我们先考虑非负函数的积分.

(2)、 对非负函数的积分, 有一个特别简单的情形, 那就是简单函数的积分.

(3)、 所以本章的结构如下: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \S 2 &\mbox{考虑非负简单函数的 Lebesgue 积分},\\ \S 3 &\mbox{考虑非负可测函数的 Lebesgue 积分},\\ \S 4 &\mbox{考虑一般可测函数的 Lebesgue 积分},\\ \S 5 &\mbox{指出 Riemann 积分与 Lebesgue 积分的关系},\\ \S 6 &\mbox{推广 Fubini 定理--累次积分, 将高维 Lebesgue 积分计算转化为低维情形.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.2. 非负简单函数的 Lebesgue 积分

05.2.1. 非负简单函数 Lebesgue 积分的定义与例子

---

1、 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \phi(x)=\sum_{i=1}^j c_i\chi_{E_i}(x),\quad c_i\gt 0, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

其中 $\displaystyle E_i$ 可测, $\displaystyle E_i$ 两两不交, $\displaystyle E=\bigcup_{i=1}^j E_i$, 则定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_E \phi(x)\mathrm{ d} x=\sum_{i=1}^j c_i\cdot mE_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 若 $A(\subset E)$ 可测, 则定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_A\phi(x)\mathrm{ d} x=\sum_{i=1}^j c_i\cdot m(E_i\cap A). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 例. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D(x)=\left\{\begin{array}{ll} 1,&x\in\mathbb{Q},\\ 0,&x\in\mathbb{R}\backslash \mathbb{Q} \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

的 Lebesgue 积分为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_{\mathbb{R}}D(x)\mathrm{ d} x &=1\cdot m(\mathbb{Q})+0\cdot m(\mathbb{R}\backslash \mathbb{Q})\\ &=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.2.2. 非负简单函数 Lebesgue 积分的性质

设 $\displaystyle \phi(x),\psi(x)$ 为非负简单函数.

---

1、 正齐次性. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} c\gt 0\Rightarrow \int_Ec\phi(x)\mathrm{ d} x =c\int_E \phi(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 有限可加性. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_E[\phi(x)+\psi(x)]\mathrm{ d} x =\int_E \phi(x)\mathrm{ d} x +\int_E \psi(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 单调性. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \phi(x)\leq \psi(x)\Rightarrow \int \phi(x)\mathrm{ d} x\leq \int \psi(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 对积分区域的有限可加性. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &A,B(\subset E)\mbox{ 无交可测}\\ \Rightarrow& \int_{A\cup B}\phi(x)\mathrm{ d} x =\int_A\phi(x)\mathrm{ d} x +\int_B\phi(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 单增积分区域的极限. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &A_k(\subset E)\mbox{ 单增}\\ \Rightarrow& \lim_{k\to\infty}\int_{A_k}\phi(x)\mathrm{ d} x =\int_{\lim_{k\to\infty}A_k}\phi(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.3. 非负可测函数的 Lebesgue 积分

05.3.1. 非负可测函数的 Lebesgue 积分的定义

本节中, 设 $\displaystyle f,g,f_i$ 是可测集 $\displaystyle E$ 上的非负可测函数; $\displaystyle A,B$ 是 $\displaystyle E$ 的可测子集; $\displaystyle \alpha,\beta\gt 0$.

---

1、 对可测集 $E$ 上的非负可测函数 $\displaystyle f$, 怎么定义 $f$ 在 $\displaystyle E$ 上的 $\displaystyle \mathscr{L}$ 积分呢? 据 $\displaystyle \S 4.1$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ \mbox{非负简单函数列 }\varphi_k\nearrow f. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而自然定义

$$\begin{equation}\tag{5.3: def: limit}\label{5.3: def: limit}\begin{aligned} \int_E f(x)\mathrm{ d} x =\lim_{k\to\infty} \int_E \varphi_k(x)\mathrm{ d} x. \end{aligned}\end{equation}$$

---

2、 可以证明

$$\begin{equation}\tag{5.3: def: sup}\label{5.3: def: sup}\begin{aligned} &\lim_{k\to\infty}\int_E \varphi_k(x)\mathrm{ d} x\\ =&\sup\left\{\int_E\phi(x)\mathrm{ d} x; 0\leq \phi\leq f\right\}. \end{aligned}\end{equation}$$

而也可定义 像大多数书上那样 $f$ 在 $\displaystyle E$ 上的 Lebesgue 积分为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_E f(x)\mathrm{ d} x \stackrel{\rm def}{=}\sup\left\{\int_E\phi(x)\mathrm{ d} x; 0\leq \phi\leq f\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\displaystyle f$ 在 $\displaystyle E$ 上 Lebesgue 可积 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \stackrel{\rm def}{\Leftrightarrow} \int_Ef(x)\mathrm{ d} x\lt +\infty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

记作 $\displaystyle f\in \mathscr{L}(E)$.

---

4、 $f$ 在 $\displaystyle A$ 上的 Lebesgue 积分为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_A f(x)\mathrm{ d} x =\int_E f(x)\chi_A(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.3.2. 非负可测函数 Lebesgue 积分的基本性质

---

1、 底面积为零蕴含体积为零 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} mE=0\Rightarrow \int_Ef(x)\mathrm{ d} x=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 非负 Lebesgue 积分为零蕴含被积函数几乎处处为零 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_Ef(x)\mathrm{ d} x=0\Rightarrow f(x)=0,\mbox{a.e.}\mbox{于}E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 非负 Lebesgue 积分有限蕴含被积函数几乎处处有限 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_Ef(x)\mathrm{ d} x\lt +\infty\Rightarrow 0\leq f(x)\lt +\infty,\mbox{a.e.}\mbox{于}E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 关于积分区域的可加性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &A\cap B=\varnothing\\ \Rightarrow&\int_{A\cup B}f(x)\mathrm{ d} x=\int_A f(x)\mathrm{ d} x+\int_Bf(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 关于被积函数的单调性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\leq g\mbox{a.e.}\Rightarrow \int_E f(x)\mathrm{ d} x \leq\int_E g(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 非负可测函数几乎处处相等蕴含积分相等 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f=g,\mbox{a.e.}\Rightarrow \int_E f(x)\mathrm{ d} x=\int_E g(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

特别地, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f=0,\mbox{a.e.}\Rightarrow \int_Ef(x)\mathrm{ d} x=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 例. 非负可测函数几乎处处相等蕴含积分相等的应用 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\left\{\begin{array}{llllllllllll} x^2,&x\in \mathbb{Q}\\ \frac{1}{x^2+2},&x\in\mathbb{R}\backslash \mathbb{Q} \end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

试证: $\displaystyle f$ 在 $\displaystyle \mathbb{R}$ 上非负可测, 并求 $\displaystyle \int_\mathbb{R} f(x)\mathrm{ d} x$.

05.3.3. 非负可测函数 Lebesgue 积分的重要性质1: Levi 引理

---

1、 Levi 引理: 非负递增可测蕴含积分与极限可交换 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &0\leq f_i\mbox{ 单增}, \lim_{i\to\infty}f_i=f\\ \Rightarrow& \lim_{i\to\infty}\int_E f_i(x)\mathrm{ d} x =\int_E f(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. Levi 引理的应用 试求 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{k\to\infty}\int_0^{\frac{\pi}{2}}\sin^kx\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Levi 引理的推论: 正线性性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\int_E[\alpha f(x)+\beta g(x)]\mathrm{ d} x\\ =&\alpha \int_E f(x)\mathrm{ d} x +\beta \int_E g(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. 设 $\left\{E_i\right\}_{i=1}^j\ (\subset [0,1])$ 可测, $\displaystyle [0,1]$ 中任一点均属于 $\displaystyle \left\{E_i\right\}_{i=1}^j$ 中的 $\displaystyle q$ 个, 则 $\displaystyle \exists\ i_0,\mathrm{ s.t.} mE_{i_0}\gt q/j$.

05.3.4. 非负可测函数 Lebesgue 积分的重要性质2: 逐项积分

---

1、 逐项积分: 对非负可测函数列, 求和与积分可交换 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_i\gt 0\Rightarrow \int_E \sum_{i=1}^\infty f_i(x)\mathrm{ d} x =\sum_{i=1}^\infty \int_Ef_i(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. 逐项积分的应用 设 $\left\{r_k\right\}$ 是 $\displaystyle [0,1]$ 中的全体有理数, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \sum_{k=1}^\infty \frac{1}{k^2\sqrt{|x-r_k|}}\mbox{a.e.}\mbox{ 收敛}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 例. 逐项积分的应用 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\sum_{k=1}^\infty \frac{k}{3^k}\chi_{[k,k+1)}(x),\ x\in [1,\infty), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

试求 $\displaystyle \int_{[1,\infty)}f(x)\mathrm{ d} x$.

05.3.5. 非负可测函数 Lebesgue 积分的重要性质3: Fatou 引理

---

1、 Fatou 引理: 非负可测函数列下极限的积分小于等于积分的下极限 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f_i\gt 0\Rightarrow \int_E \varliminf_{i\to\infty}f_i(x)\mathrm{ d} x\leq \varliminf_{i\to\infty}\int_Ef_i(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 例. Fatou 引理的应用 求 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}\int_0^\frac{\pi}{2} (-\sin x)^n\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.4. 一般可测函数的 Lebesgue 积分

05.4.1. 一般可测函数 Lebesgue 积分的定义

本节中, 设 $f,g,f_i$ 是可测集 $\displaystyle E$ 上的可测函数; $\displaystyle A,B(\subset E)$ 可测; $\displaystyle \alpha,\beta\in\mathbb{R}$.

---

1、 $f$ 在 $\displaystyle E$ 上积分确定 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \stackrel{\rm def}{\Leftrightarrow} \int_Ef^+(x)\mathrm{ d} x\lt +\infty\mbox{或}\int_Ef^-(x)\mathrm{ d} x\lt +\infty \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

此时称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_E f(x)\mathrm{ d} x=\int_Ef^+(x)\mathrm{ d} x -\int_Ef^-(x)\mathrm{ d} x \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle f$ 在 $\displaystyle E$ 上的 Lebesgue 积分.

---

2、 $\displaystyle f$ 在 $\displaystyle E$ 上 Lebesgue 可积 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \stackrel{\rm def}{\Leftrightarrow}\int_Ef^+(x)\mathrm{ d} x\lt +\infty\mbox{且}\int_Ef^-(x)\mathrm{ d} x\lt +\infty. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\displaystyle E$ 上 Lebesgue 可积的函数全体记作 $\displaystyle \mathscr{L}(E)$.

05.4.2. 一般可测函数 Lebesgue 积分的基本性质

---

1、 底面积为零蕴含体积为零 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &E\neq \varnothing, mE=0\\ \Rightarrow& f\in \mathscr{L}(E), \mbox{且}\int_Ef(x)\mathrm{ d} x=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Lebesgue 可积蕴含被积函数几乎处处有限 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{L}(E)\Rightarrow f\mbox{a.e.} \mbox{有限, 于}E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $f$ 在 $\displaystyle E$ 上积分确定 $\displaystyle \Rightarrow f$ 在 $\displaystyle A$ 上积分确定.

---

4、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ \left\{\begin{array}{ll} f\mbox{ 在 }E\mbox{ 上积分确定}\\ E=A\cup B,\ A\cap B=\varnothing\end{array}\right.\\ & \Rightarrow \int_E f(x)\mathrm{ d} x =\int_Af(x)\mathrm{ d} x+\int_Bf(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 关于积分区域的可数可加性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll}E=\bigcup_{i=1}^\infty E_i,\ E_i\mbox{ 两两不交}\\ f\mbox{ 在 }E\mbox{ 上积分确定} \end{array}\right.\\ \Rightarrow& \int_E f(x)\mathrm{ d} x =\sum_{i=1}^\infty \int_{E_i}f(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll}f\mbox{ 在 }E\mbox{ 上积分确定}\\ f=g,\mbox{a.e.}\mbox{ 于 }E\end{array}\right.\\ \Rightarrow&\left\{\begin{array}{ll} g\mbox{ 在 }E\mbox{ 上积分确定}\\ \int_E g(x)\mathrm{ d} x=\int_E f(x)\mathrm{ d} x\end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll}f,g\mbox{ 在 }E\mbox{ 上积分确定}\\ f\leq g\mbox{a.e.}\mbox{ 于 }E\end{array}\right.\\ \Rightarrow& \int_E f(x)\mathrm{ d} x\leq \int_E g(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

8、 积分估值 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \left\{\begin{array}{ll} mE\lt +\infty\\ b\leq f\leq B,\mbox{a.e.}\mbox{ 于 }E \end{array}\right.\\ &\Rightarrow b\cdot mE\leq \int_E f(x)\mathrm{ d} x \leq B\cdot mE. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

9、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ \left\{\begin{array}{ll} 0\leq g\in \mathscr{L}(E)\\ |f|\leq g,\ \mbox{a.e.}\mbox{ 于 }E \end{array}\right.\\ &\Rightarrow\left\{\begin{array}{ll} f\in \mathscr{L}(E)\\ \left|\int_Ef(x)\mathrm{ d} x\right|\leq \int_E |f(x)|\mathrm{ d} x \leq \int_Eg(x)\mathrm{ d} x \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

10、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{L}(E) \Rightarrow\left\{\begin{array}{ll} \alpha f\in \mathscr{L}(E)\\ \int_E \alpha f(x)\mathrm{ d} x=\alpha \int_E f(x)\mathrm{ d} x \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

11、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f,g\in \mathscr{L}(E)\\ \Rightarrow& \left\{\begin{array}{ll} f+g\in \mathscr{L}(E)\\ \int_E[f+g]\mathrm{ d} x =\int_E f\mathrm{ d} x +\int_E g\mathrm{ d} x \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

12、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f,g\in \mathscr{L}(E)\\ \Rightarrow&\left\{\begin{array}{llllllllllll} \alpha f+\beta g\in \mathscr{L}(E)\\ \int_E [\alpha f+\beta g]\mathrm{ d} x =\alpha\int_E f\mathrm{ d} x +\beta\int_E g\mathrm{ d} x\end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.4.3. 一般可测函数 Lebesgue 积分的重要性质1: 函数可积等价于其绝对值可积

---

1、 我们学过的函数性质, 函数及其绝对值的表现完全不同.

(1)、 证明: 若 $\displaystyle f$ 在 $\displaystyle x_0$ 处连续, 则 $\displaystyle |f|$ 在 $\displaystyle x_0$ 处连续. 举例说明反之不成立. 参考解答

(2)、 举例说明: $\displaystyle f$ 在 $\displaystyle x_0$ 处可导, 但 $\displaystyle |f|$ 在 $\displaystyle x_0$ 处不可导. 反之也不对. 证明: 如果 $\displaystyle f$ 在 $\displaystyle x_0$ 处连续, $\displaystyle |f|$ 在 $\displaystyle x_0$ 处可导, 则 $\displaystyle f$ 在 $\displaystyle x_0$ 处可导. 参考解答

(3)、 证明: 若 $\displaystyle f$ 在 $\displaystyle [a,b]$ 上黎曼可积, 则 $\displaystyle |f|$ 在 $\displaystyle [a,b]$ 上黎曼可积. 举例说明反之不成立. 参考解答

(4)、 证明: 若 $\displaystyle |f|$ 在 $\displaystyle [a,+\infty)$ 上的无穷限积分存在, 则 $\displaystyle f$ 在 $\displaystyle [a,+\infty)$ 上的无穷限积分存在. 举例说明反之不成立. 参考解答

(5)、 证明: 若 $\displaystyle f$ 在可测集 $\displaystyle E$ 上是可测函数, 则 $\displaystyle |f|$ 也是 $\displaystyle E$ 上的可测函数. 但反之不成立. 参考解答

---

2、 但是对于 Lebesgue 可积这个性质, 能完全颠覆我们的想象. 也许你一辈子只能见到的唯一性质.

---

3、 $\displaystyle f\in \mathscr{L}(E)\Leftrightarrow|f|\in \mathscr{L}(E)$, 且有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left|\int_Ef(x)\mathrm{ d} x\right|\leq \int_E |f(x)|\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.4.4. 一般可测函数 Lebesgue 积分的重要性质2: 绝对连续性

---

1、 绝对连续? 没听过. 确实. 第 6 章我们还会再看.

(1)、 相信大家都知道连续, $[a,b]$ 上的连续函数全体记作 $\displaystyle C[a,b]$. 那 Lipschitz 连续呢? 哦, 对, ODE 讲过. 函数 $f: [a,b]\to\mathbb{R}$ 称为 Lipschitz 连续, 如果 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ L\gt 0,\mathrm{ s.t.} \forall\ x,y\in [a,b], |f(x)-f(y)|\leq L|x-y|. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\displaystyle [a,b]$ 上的全体 Lipschitz 函数记作 $\displaystyle Lip[a,b]$.

(2)、 我们有如下的包含关系: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} C^1[a,b]\subset Lip[a,b]\subset C[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这里, $C^1[a,b]$ 表示 $\displaystyle [a,b]$ 上的连续可微函数全体.

(3)、 现在, 我们要讲的绝对连续呢? 就介于 Lip 与 C 之间.

---

2、 积分的绝对连续性 (absolute continuity): 积分值是被积可测集测度的连续函数: $\displaystyle f\in \mathscr{L}(E)$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \Rightarrow \left[\forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\ \forall\ A\subset E: mA\lt \delta,\atop\mbox{ 有 }\left|\int_A f(x)\mathrm{ d} x\right| \leq \int_A|f(x)|\mathrm{ d} x\lt \varepsilon.\right] \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.4.5. 一般可测函数 Lebesgue 积分的重要性质3: Lebesgue控制收敛及其推论

---

1、 Lebesgue 控制收敛定理 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{llllllllllll}\begin{array}{ll} |f_i|\leq F,\quad F\in \mathscr{L}(E)\\ f_i\to f,\mbox{a.e.}\mbox{ 于 }E \end{array}\end{array}\right.\\ \Rightarrow&\left\{\begin{array}{ll} \lim_{i\to\infty}\int_E|f_i(x)-f(x)|\mathrm{ d} x=0\\ \lim_{i\to\infty}\int_E f_i(x)\mathrm{ d} x =\int_E f(x)\mathrm{ d} x. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Lebesgue 控制收敛定理的应用 求 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}\int_1^2 \left[\frac{(x-1)^\frac{1}{n}+(2-x)^\frac{1}{n}}{2}\right]^n\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 依测度控制收敛 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll} |f_i|\leq F,\quad F\in \mathscr{L}(E)\\ f_i\Rightarrow f \end{array}\right.\\ \Rightarrow&\left\{\begin{array}{ll} \lim_{i\to\infty}\int_E|f_i(x)-f(x)|\mathrm{ d} x=0\\ \lim_{i\to\infty}\int_E f_i(x)\mathrm{ d} x =\int_E f(x)\mathrm{ d} x. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 逐项积分 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll} f_i\in \mathscr{L}(E)\\ \sum_{i=1}^\infty \int_E|f_i(x)|\mathrm{ d} x\lt +\infty \end{array}\right.\\ \Rightarrow&\left\{\begin{array}{ll} \sum_{i=1}^\infty f_i(x)\mbox{a.e.} \mbox{ 绝对收敛, 于 }E\\ \int_E\sum_{i=1}^\infty f_i(x)\mathrm{ d} x =\sum_{i=1}^\infty \int_Ef_i(x)\mathrm{ d} x. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 求导与积分交换次序: 设 $\displaystyle f(x,t)$ 是 $\displaystyle E\times (a,b)$ 上的实函数, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ \left\{\begin{array}{ll} f(\cdot,t)\in \mathscr{L}(E),\quad \forall\ t\\ f(x,\cdot)\mbox{ 可导}, \left|\frac{\partial f}{\partial t}(x,\cdot)\right|\leq F(x),\mbox{a.e.}\mbox{于}E,\quad F\in \mathscr{L}(E) \end{array}\right.\\ &\Rightarrow \frac{\mathrm{ d}}{\mathrm{ d} t}\int_E f(x,t)\mathrm{ d} x =\int_E \frac{\partial}{\partial t}f(x,t)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.4.6. 应用: Lebesgue 可积函数的连续函数逼近

---

1、 逼近很重要? 为啥? 从特殊到一般呗.

(1)、 Weierstrass 第一逼近定理: $\displaystyle [a,b]$ 上的连续函数可由多项式函数列一致逼近.

(2)、 Weierstrass 第二逼近定理: $\displaystyle \mathbb{R}$ 上的周期函数可由三角函数列一致逼近.

(3)、 非负可测函数: 可由简单函数列递增逼近.

(4)、 有界可测函数: 可由简单函数列一致逼近.

(5)、 一般可测函数: 可由简单函数列逐点逼近, 与连续函数基本上相等.

---

2、 Lebesgue 可积函数可由连续函数在积分意义下逼近 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \ f\in \mathscr{L}[a,b]\\ &\Rightarrow \boxed{\begin{array}{c}\forall\ \varepsilon\gt 0,\ \exists\ g\in C[a,b],\mathrm{ s.t.}\\ \int_{[a,b]}|f(x)-g(x)|\mathrm{ d} x\lt \varepsilon.\end{array}} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.5. Riemann 积分和 Lebesgue 积分

05.5.1. 回忆 Riemann 积分

---

1、 记号: 一元函数 $\displaystyle f$ 在 $\displaystyle [a,b]$ 上的

(1)、 Riemann 积分: $\displaystyle \int_a^b f(x)\mathrm{ d} x$;

(2)、 Lebesgue 积分: $\int_{[a,b]}f(x)\mathrm{ d} x$.

---

2、 Riemann 积分: 对函数 $f: [a,b]\to \mathbb{R}$ 及 $\displaystyle [a,b]$ 的任一分划 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &T: \ a=x_0\lt x_1\lt \cdots\lt x_n=b,\\ &\left(\mbox{细度 }\left\Vert T\right\Vert =\max_i\Delta x_i\right), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 Darboux 上、下和: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} U_{f,T}\stackrel{\rm def}{=}\sum_{i=1}^n M_i\Delta x_i,&\quad M_i\stackrel{\rm def}{=}\sup_{[x_{i-1},x_i]}f,\\ L_{f,T}\stackrel{\rm def}{=}\sum_{i=1}^n m_i\Delta x_i,&\quad m_i\stackrel{\rm def}{=}\inf_{[x_{i-1},x_i]}f, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而显然有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &T\subset T'\Rightarrow U_{f,T}\gt U_{f,T'},\quad L_{f,T}\leq L_{f,T'}; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

分划越细, Darboux 上和越小, Darboux 下和越大 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T,T'\Rightarrow L_{f,T}\leq U_{f,T'}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

不同的分划, Darboux 下和 $\displaystyle \leq$ Darboux 上和 再定义 Darboux 上、下积分: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overset{-}{\int_a^b} f(x)\mathrm{ d} x\stackrel{\rm def}{=}&\inf_T U_{f,T},\\ \underset{-}{\int_a^b}f(x)\mathrm{ d} x\stackrel{\rm def}{=}&\sup_T L_{f,T}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而显然有 $\displaystyle \overset{-}{\int_a^b} f(x)\mathrm{ d} x\gt \underset{-}{\int_a^b}f(x)\mathrm{ d} x.$ 最后定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f&\in \mathscr{R}[a,b]\stackrel{\rm def}{\Leftrightarrow} \overset{-}{\int_a^b} f(x)\mathrm{ d} x= \underset{-}{\int_a^b}f(x)\mathrm{ d} x\\ &\Leftrightarrow \exists\ T^{(n)}_1,T^{(n)}_2: \left\Vert T^{(n)}_1\right\Vert ,\left\Vert T^{(n)}_2\right\Vert \to 0,\mathrm{ s.t.}\\ &\quad \quad U_{f,T^{(n)}_1}\searrow I,\ L_{f,T^{(n)}_2}\nearrow I\\ &\quad \left(I\stackrel{\rm def}{=}\int_a^b f(x)\mathrm{ d} x\right)\\ &\Leftrightarrow \exists\ T^{(n)}=T^{(n)}_1\cup T^{(n)}_2: \ \left\Vert T^{(n)}\right\Vert \to 0,\mathrm{ s.t.}\\ &\quad \quad \lim_{n\to\infty}\left[U_{f,T^{(n)}}-L_{f,T^{(n)}}\right]=0\\ &\Leftrightarrow \exists\ T^{(n)}: \ 0=x^{(n)}_0\lt x^{(n)}_1\lt \cdots\lt x^{(n)}_{P_n}: \\ &\quad \ \left\Vert T^{(n)}\right\Vert \to 0,\\ &\quad \ \mathrm{ s.t.}\lim_{n\to\infty}\sum_{i=1}^{P_n}\left[M^{(n)}_i-m^{(n)}_i\right]\Delta x_i=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注意: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E=\bigcup_{n=1}^\infty T^{(n)}=\bigcup_{n=1}^\infty \left\{x^{(n)}_0,x^{(n)}_1,\cdots,x^{(n)}_{P_n}\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

可数, 而是零测度集.

05.5.2. 连续函数的振幅刻画

---

1、 连续函数的振幅刻画 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\mbox{ 在 }x\mbox{ 处连续}\\ \Leftrightarrow& \omega(x)\stackrel{\rm def}{=} \lim_{\delta\to 0 } \sup_{x',x))\in U(x;\delta)\cap [a,b]}|f(x')-f(x)))|=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.5.3. Riemann 可积函数的刻画

---

1、 Riemann 可积函数的刻画 设 $\displaystyle f: [a,b]\to \mathbb{R}$ 有界, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{R}[a,b]\Leftrightarrow f\mbox{a.e.} \mbox{ 连续, 于 }[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 为证 $\displaystyle h_n(x)\to \omega(x),x\in [a,b]\backslash E$, 仅须注意到 $\left\Vert T^{(n)}\right\Vert \to 0$ 及 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \omega(x)&=\lim_{n\to\infty} \sup_{x^{(n)}_{i_n-1}\lt x',x''\lt x^{(n)}_{i_n}}|f(x')-f(x'')|\\\ &\quad \left(\mbox{不在乎是否为中央开区间}\right)\\ &=\lim_{n\to\infty}[M^{(n)}_{i_n}-m^{(n)}_{i_n}]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

最后一步你学过的. 参见 华东师大数学分析第五版1.5.16

---

3、 本定理也有纯数学分析的证明, 参考常庚哲, 史济怀 编著 数学分析教程 上册第三版第 6.6 节. 那里讲得也蛮详细的哦.

05.5.4. Lebesgue 积分是 Riemann 积分的推广

---

1、 设 $\displaystyle f: [a,b]\to \mathbb{R}$ 注意: $\displaystyle f\in \mathscr{R}[a,b]\Rightarrow f$ 有界, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{R}[a,b]\Rightarrow \left\{\begin{array}{llllllllllll}f\in \mathscr{L}[a,b],\\ \mbox{且} \int_{[a,b]}f(x)\mathrm{ d} x = \int_a^b f(x)\mathrm{ d} x.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.5.5. Lebesgue 积分是非负 Riemann 反常积分的推广

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll} f: [a,\infty)\to [0,\infty)\\ f\in R[a,A],\quad \forall\ A\gt a\\ \int_a^{\infty}f(x)\mathrm{ d} x\mbox{ 收敛} \end{array}\right.\\ \Rightarrow&\left\{\begin{array}{ll} f\in \mathscr{L}[a,\infty)\\ \int_{[a,\infty)}f(x)\mathrm{ d} x =\int_a^{\infty}f(x)\mathrm{ d} x. \end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.5.6. Lebesgue 积分不是 Riemann 反常积分的推广

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\left\{\begin{array}{ll} \frac{\sin x}{x},&x\in (0,\infty)\\ 1,&x=0 \end{array}\right.\Rightarrow \left\{\begin{array}{llllllllllll} f\in \mathscr{R}[0,\infty)\\ f\not\in \mathscr{L}[0,\infty) \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.6. Lebesgue 积分的几何意义, Fubini 定理

05.6.1. 直积与截面

---

1、 从低维到高维 对 $\displaystyle A\subset \mathbb{R}^p, B\subset\mathbb{R}^q$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A\times B=\left\{(x,y);x\in A, y\in B\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 $A$ 与 $\displaystyle B$ 的直积 (direct product).

---

2、 从高维到低维 设 $\displaystyle E\subset \mathbb{R}^{p+q}$, $x\in \mathbb{R}^p$, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} E_x=\left\{y\in\mathbb{R}^q;(x,y)\in E\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $E$ 关于 $\displaystyle x$ 的截面 (section).

---

3、 直积与截面的性质 说白了, 就是直积/截面保持包含, 无交, 并, 交, 差等运算 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A_1\subset A_2&\Rightarrow\left\{\begin{array}{llllllllllll} (A_1\times B)\subset( A_2\times B)\\ (A_1)_x\subset (A_2)_x\end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A_1\cap A_2=\varnothing&\Rightarrow \left\{\begin{array}{llllllllllll} (A_1\times B)\cap( A_2\times B)=\varnothing\\ (A_1)_x\cap (A_2)_x=\varnothing\end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{A_i\right\}_i&\Rightarrow\left\{\begin{array}{llllllllllll}\left(\bigcup_iA_i\right)\times B=\bigcup_i (A_i\times B)\\ \left(\bigcup_i A_i\right)_x=\bigcup_i (A_i)_x\end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{A_i\right\}_i&\Rightarrow\left\{\begin{array}{llllllllllll}\left(\bigcap_iA_i\right)\times B=\bigcap_i (A_i\times B)\\ \left(\bigcap_i A_i\right)_x=\bigcap_i (A_i)_x\end{array}\right., \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{\begin{array}{llllllllllll}(A_1\backslash A_2)\times B=(A_1\times B)\backslash (A_2\times B)\\ (A_1\backslash A_2)_x=(A_1)_x\backslash (A_2)_x\end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 直积保持开、闭: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} O_1,\ O_2\mbox{ 开 }&\Rightarrow O_1\times O_2\mbox{ 开};\\ F_1,\ F_2\mbox{ 闭}&\Rightarrow F_1\times F_2\mbox{ 闭}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.6.2. 降维法求测度: Fubini 定理的前奏

---

1、 截面定理 设 $\displaystyle E\subset \mathbb{R}^{p+q}$ 可测, 则

(1)、 对 $\displaystyle \mbox{a.e.} x\in \mathbb{R}^p$, $E_x\subset \mathbb{R}^q$ 可测;

(2)、 $\displaystyle mE_x$ 是 $\displaystyle \mathbb{R}^p$ 上 $\displaystyle \mbox{a.e.}$ 有定义的可测函数;

(3)、 $\displaystyle mE=\int_{\mathbb{R}^p}mE_x\mathrm{ d} x$.

---

2、 直积的测度: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &A\subset\mathbb{R}^p\mbox{ 可测}, B\subset \mathbb{R}^q\mbox{ 可测}\\ \Rightarrow& \left\{\begin{array}{llllllllllll}A\times B\subset\mathbb{R}^{p+q}\mbox{ 可测,}\\ \mbox{且} m(A\times B)=mA\cdot mB.\end{array}\right. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.6.3. 非负可测函数积分的几何意义

---

1、 设 $f$ 为可测集 $\displaystyle E\subset \mathbb{R}^n$ 上的非负函数. 则

(1)、 $\displaystyle f$ 在 $\displaystyle E$ 上可测 $\displaystyle \Leftrightarrow$ $f$ 的下方图形 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} G(E,f)=\left\{(x,z);x\in E,0\leq z\lt f(x)\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

在 $\displaystyle \mathbb{R}^n$ 中可测;

(2)、 $\displaystyle f$ 在 $\displaystyle E$ 上可测 $\displaystyle \Rightarrow\int_Ef(x)\mathrm{ d} x =mG(E,f)$.

---

2、 推广: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{llllllllllll}E\subset \mathbb{R}^n\\ f\in \mathscr{L}(E)\end{array}\right.\\ \Rightarrow& \int_E f(x)\mathrm{ d} x=mG(E,f^+)-mG(E,f^-). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $f$ Lebesgue 可积的一个充要条件 上、下方图形的面积均有限: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{L}(E)\Leftrightarrow mG(E,f^\pm)\lt +\infty. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

05.6.4. Fubini 定理与累次积分

---

1、 Fubini 定理:

(1)、 设 $\displaystyle f(P)=f(x,y)$ 在可测集 $\displaystyle A\times B\subset \mathbb{R}^p\times \mathbb{R}^q$ 上非负可测, 则对 $\displaystyle \mbox{a.e.} x\in A$, $f(x,y)$ 作为 $\displaystyle y$ 的函数在 $\displaystyle B$ 上非负可测, 且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_{A\times B}f(P)\mathrm{ d} P =\int_A\mathrm{ d} x\int_Bf(x,y)\mathrm{ d} y. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 设 $\displaystyle f(P)=f(x,y)$ 在可测集 $\displaystyle A\times B\subset \mathbb{R}^p\times \mathbb{R}^q$ 上可积, 则对 $\displaystyle \mbox{a.e.} x\in A$, $f(x,y)$ 作为 $\displaystyle y$ 的函数在 $\displaystyle B$ 上可积, $\displaystyle \int_B f(x,y)\mathrm{ d} y$ 作为 $\displaystyle x$ 的函数在 $\displaystyle A$ 上可积, 且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_{A\times B}f(P)\mathrm{ d} P =\int_A\mathrm{ d} x\int_Bf(x,y)\mathrm{ d} y. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{重积分存在}\Rightarrow \mbox{累次积分相等}\Rightarrow \mbox{ 累次积分可交换次序}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Fubini 定理的应用 $\displaystyle E=(0,1)^2$ 上的函数 $\displaystyle f(x,y)=\frac{x^2-y^2}{(x^2+y^2)^2}$, 由 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \int_{(0,1)}\mathrm{ d} x\int_{(0,1)}f(x,y)\mathrm{ d} y &=\frac{\pi}{4},\\ \int_{(0,1)}\mathrm{ d} y\int_{(0,1)}f(x,y)\mathrm{ d} x&=-\frac{\pi}{4} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

知 $f\not\in \mathscr{L}(E)$.

05.7. 本章小结

---

1、 非负简单函数的 Lebesgue 积分 (底乘以高).

---

2、 非负可测函数的 Lebesgue 积分 (最重要的定理: Levi 引理, 逐项积分, Fatou 引理).

---

3、 一般可测函数的 Lebesgue 积分 (最重要的定理: Lebesgue 控制收敛定理, Lebesgue 积分的绝对连续性, 逐项积分).

---

4、 Rieman 积分与 Lebesgue 积分的关系.

---

5、 Fubini 定理 (非负可测时, 一般可测时).

06. 微分与不定积分 (differentiability and indefinite integral

06.0. 引言

---

1、 数学分析中有积分与微分的互逆运算: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{R}[a,b]&\Rightarrow f\mbox{a.e.} \mbox{ 连续}\\ &\Rightarrow\frac{\mathrm{ d} }{\mathrm{ d} x}\int_a^x f(t)\mathrm{ d} t =f(x),\mbox{a.e.}\\ &\Rightarrow \mbox{积分后微分可 }\mbox{a.e.}\mbox{ 还原};\\ f'\in \mathscr{R}[a,b]&\Rightarrow f(x)=f(a)+\int_a^xf'(t)\mathrm{ d} t\\ &\Rightarrow\mbox{微分后再积分可还原}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 本章主要把上述积分与微分的互逆运算推广到 Lebesgue 积分的情形.

06.1. Vitali 定理

---

1、 $V$-覆盖: 设 $E\subset \mathbb{R}$, $\mathscr{V}=\left\{I;|I|\gt 0\right\}$. 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \forall\ x\in E,\ \forall\ \varepsilon\gt 0,\ \exists\ I\in \mathscr{V},\mathrm{ s.t.} x\in I,\ |I|\lt \varepsilon\\ &\Leftrightarrow \forall\ x\in E,\ \exists\ I_n\in \mathscr{V},\mathrm{ s.t.} x\in I_n, mI_n\to 0, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\mathscr{V}$ 是 $\displaystyle E$ 的 $\displaystyle V$-覆盖.

---

2、 Vitali 覆盖定理---可数不交几乎覆盖: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll} E\subset \mathbb{R}: m^\star E\lt +\infty\\ \mathscr{V}\mbox{ 是 } E\mbox{ 的 }V\mbox{- 覆盖} \end{array}\right.\\ \Rightarrow& {\exists\ \left\{I_k\right\}_{k=1}^\infty\mbox{ 两两不交},\atop\mathrm{ s.t.} m\left(E\backslash \bigcup_{k=1}^\infty I_k\right)=0.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Vitali 覆盖定理的另一形式---有限不交基本上覆盖: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{\begin{array}{ll} E\subset\mathbb{R}: m^\star E\lt +\infty\\ \mathscr{V}\mbox{ 是 }E\mbox{ 的 }V\mbox{- 覆盖} \end{array}\right.\\ \Rightarrow& {\forall\ \varepsilon\gt 0,\ \exists\ \left\{I_k\right\}_{k=1}^n \mbox{ 两两不交},\atop\mathrm{ s.t.} m\left(E\backslash \bigcup_{k=1}^n E_k\right)\lt \varepsilon.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

06.2. 单调函数的可微性

---

1、 列导数: 设 $f: [a,b]\to \mathbb{R}$, $x_0\in [a,b]$. 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ 0\neq h_n\to 0,\mathrm{ s.t.} \lim_{n\to\infty}\frac{f(x+h_n)-f(x)}{h_n}=\lambda \mbox{ 或 }\pm \infty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\lambda$ 为 $\displaystyle f$ 在 $\displaystyle x_0$ 处的一个列导数, 记作 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} Df(x_0)=\lambda. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(1)、 当 $\displaystyle f'(x)$ 存在时, $\displaystyle Df(x)=f'(x)$.

(2)、 $Df(x_0)$ 与 $\displaystyle h_n$ 的选取有关: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D|x|(0)&=\left\{\begin{array}{ll} -1,&h_n\lt 0\\ 1,&h_n\gt 0 \end{array}\right.;\\ DD(r)&=\left\{\begin{array}{ll} 0,&h_n\in \mathbb{Q}\\ -\infty,&0\lt h_n\not\in \mathbb{Q}\\ +\infty,&0\gt h_n\not\in \mathbb{Q} \end{array}\right.,\quad r\in\mathbb{Q}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 外测度在映射下的变化: 设 $\displaystyle f$ 在 $\displaystyle [a,b]$ 上严格单增, $\displaystyle E\subset [a,b]$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &Df(x)\leq p\ (p\gt 0),\ x\in E\\ \Rightarrow& m^\star f(E)\leq p\cdot m^\star E;\\ &Df(x)\gt q\ (q\gt 0),\ x\in E\\ \Rightarrow& m^\star f(E)\gt q\cdot m^\star E. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Lebesgue 关于单调函数的定理: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\mbox{ 在 }[a,b] \mbox{ 上单增}\\ \Rightarrow& \left\{\begin{array}{ll} f\mbox{a.e.} \mbox{ 存在导数}\Rightarrow f'\gt 0,\mbox{a.e.}\\ f'\mbox{非负可测}\\ f'\mbox{ 在 }[a,b]\mbox{ 上 Lebesgue 可积}\\ \int_a^b f'(x)\mathrm{ d} x\leq f(b)-f(a) \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

06.3. 有界变差函数 (functions of bounded variation)

---

1、 可求长 (rectifiable) 曲线: 一条曲线 (curve) $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} C: \left\{\begin{array}{ll} x=\phi(t)\\ y=\psi(t) \end{array}\right.,\ \alpha\leq t\leq \beta \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 可求长的, 如果 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &L=\sup_{T: \alpha=t_0\lt t_1\lt \cdots\lt t_n=\beta} \sum_{i=1}^n \overline{P(t_{i-1})P(t_i)}\lt +\infty\quad \left(P(t_i)=(\phi(t_i),\psi(t_i)\right)\\ &=\sup_{T: \alpha=t_0\lt t_1\lt \cdots\lt t_n=\beta} \sum_{i=1}^n \sqrt{\boxed{\begin{array}{c}[\phi(t_i)-\phi(t_{i-1})]^2\\ +[\psi(t_i)-\psi(t_{i-1})]^2\end{array}}}\\ &\lt \infty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

或等价的, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\sup_T \sum_{i=1}^n |\phi(t_i)-\phi(t_{i-1})|\lt +\infty,\\ &\sup_T \sum_{i=1}^n |\psi(t_i)-\psi(t_{i-1})|\lt +\infty. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 有界变差函数 (functions of bounded variation): 设 $f: [a,b]\to\mathbb{R}$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\in BV[a,b]\\ \stackrel{\rm def}{\Leftrightarrow}& \bigvee_a^b(f) =\sup_T \sum_{i=1}^n|f(x_i)-f(x_{i-1})|\lt +\infty. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(1)、 例: $C$ 可求长 $\displaystyle \Leftrightarrow\ \phi,\psi\in BV[a,b]$.

(2)、 $\mathrm{Lip}[a,b]\subset BV[a,b]$.

(3)、 $\left\{[a,b]\mbox{上的单调函数}\right\}\subset BV[a,b]$.

(4)、 $BV[a,b]$ 与 $\displaystyle C[a,b]$ 之间没有半毛钱关系.

---

3、 有界变差函数的性质

(1)、 $\displaystyle f\in BV[a,b], [a_1,b_1]\subset [a,b]\Rightarrow f\in BV[a_1,b_1]$.

(2)、 $a\lt c\lt b\Rightarrow \bigvee_a^b(f)=\bigvee_a^c(f)+\bigvee_c^b(f)$.

(3)、 $f\in BV[a,b]\Rightarrow f$ 有界.

(4)、 $\displaystyle f,g\in BV[a,b]\Rightarrow f\pm g,\ f\cdot g\in BV[a,b]$. 哪个函数类也具有类似的性质呢?

---

4、 例. 利用性质计算 试求 $\bigvee_{-2}^2\left(\frac{x^4}{4}-\frac{x^2}{2}\right)$.

---

5、 注意: 我可没说 $\bigvee_a^b(f+g) =\bigvee_a^b(f)+\bigvee_a^b(g)$, 但有 $\bigvee_a^b(-f)=\bigvee_a^b(f)$.

---

6、 有界变差函数的 Jordan 分解: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in BV[a,b]\Rightarrow f=g-h,\quad g,h\nearrow. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 推论: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in BV[a,b]\Rightarrow \left\{\begin{array}{ll} f'\mbox{a.e.}\mbox{ 存在}\\ f'\in \mathscr{L}[a,b] \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

8、 $\bigvee_a^x(f)\mbox{ 单增}\Rightarrow \frac{\mathrm{ d}}{\mathrm{ d} x}\bigvee_a^x(f)=|f'(x)|,\mbox{a.e.}$.

06.4. 不定积分 (indefinite integral)

06.4.1. 不定积分及其性质

---

1、 不定积分 (indefinite integral): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{L}[a,b]\Rightarrow F(x)=\int_{[a,x]}f(t)\mathrm{ d} t+C \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 $f$ 的一个不定积分, 其中 $\displaystyle C$ 为任一常数.

---

2、 不定积分的性质: 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} F(x)=\int_{[a,x]} f(t)\mathrm{ d} t+C,\quad f\in \mathscr{L}[a,b], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则由积分的绝对连续性, $\displaystyle \forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ A\subset [a,b]: \ mA\lt \delta,\\ &\left|\int_A f(x)\mathrm{ d} x\right|\leq \int_A \left|f(x)\right|\mathrm{ d} x\lt \varepsilon. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

特别取 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A=\bigcup_{i=1}^j (a_i,b_i), &(a_i,b_i)\mbox{ 两两不交},\\ &\sum_{i=1}^j (b_i-a_i)\lt \delta, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\quad \sum_{i=1}^j |F(b_i)-F(a_i)| =\sum_{i=1}^j \left|\int_{[a_i,b_i]}f(x)\mathrm{ d} x\right|\\ & \leq \sum_{i=1}^j \int_{[a_i,b_i]}|f(x)|\mathrm{ d} x =\int_{\bigcup_{i=1}^j [a_i,b_i]}|f(x)|\mathrm{ d} x\lt \varepsilon. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

综上, 不定积分 $\displaystyle F$ 具有性质:

$$\begin{equation}\tag{6.4: ac}\label{6.4: ac}\begin{aligned} &\forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\ \forall\ \left\{(a_i,b_i)\right\}_{i=1}^j\mbox{ 两两不交},\\ &\sum_{i=1}^j (b_i-a_i)\lt \delta, \mbox{ 有 }\sum_{i=1}^j |F(b_i)-F(a_i)|\lt \varepsilon. \end{aligned}\end{equation}$$

06.4.2. 绝对连续函数及其性质

---

1、 绝对连续函数 (absolutely continuous functions): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\in AC[a,b]\\ \stackrel{\rm def}{\Leftrightarrow}& \left[ \begin{array}{c} \forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\ \forall\ \left\{(a_i,b_i)\right\}_{i=1}^j\mbox{两两不交},\\ \sum_{i=1}^j (b_i-a_i)\lt \delta, \mbox{有}\sum_{i=1}^j |F(b_i)-F(a_i)|\lt \varepsilon \end{array}\right]\mbox{ 成立}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 AC 函数的性质

(1)、 $\displaystyle f\in \mathscr{L}[a,b]\Rightarrow F(x)=\int_a^xf(t)\mathrm{ d} t+C\in AC[a,b]$.

(2)、 $AC[a,b]\subset UC[a,b]$ (uniformly continuous).

(3)、 $\displaystyle \mathrm{Lip}[a,b]\subset AC[a,b]\subset BV[a,b]$.

---

3、 常数函数的判断: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in AC[a,b],\ f'\equiv 0,\mbox{a.e.}\Rightarrow f\equiv \mathrm{const}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

06.4.3. 积分与微分为互逆运算 (Lebesgue 意义下)

---

1、 积分后再微分可还原: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f\in \mathscr{L}[a,b]\Rightarrow \frac{\mathrm{ d}}{\mathrm{ d} x}\int_{[a,x]}f(t)\mathrm{ d} t=f(x),\mbox{a.e.}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 微分后再积分可还原: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} F\in AC[a,b]\Rightarrow \left\{\begin{array}{ll} F'\mbox{a.e.}\mbox{ 存在}\\ F'\in \mathscr{L}[a,b]\\ F(x)=F(a)+\int_a^x F'(t)\mathrm{ d} t \end{array}\right.. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

06.4.4. AC 函数的进一步刻画

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &AC[a,b]=\left\{\mbox{Lebesgue 可积函数的不定积分}\right\}\\ =&\left\{f;\ \begin{array}{l}\forall\ \varepsilon\gt 0, \exists\ \delta\gt 0,\ \forall\ \left\{(a_i,b_i)\right\}_{i=1}^\infty,\\ (a_i,b_i)\mbox{ 两两不交}, \sum_{i=1}^\infty(b_i-a_i)\lt \delta,\\ \mbox{ 有 }\sum_{i=1}^\infty |f(b_i)-f(a_i)|\lt \varepsilon\end{array}\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

06.5. 本章小结

---

1、 Lebesgue 定理.

---

2、 单调函数, 有界变差函数, 连续函数, 一致连续函数, 绝对连续函数的定义, 性质及其关系.

---

3、 变差的计算.

07. 度量空间和赋范线性空间 (metric / normed linear space

07.0. 泛函分析 (functional analysis) 绪论

---

1、 泛函分析是 20 世纪发展起来的一门新的学科.

---

2、 牛人:

(1)、 希尔伯特 (D. Hilbert, 1862-1943, 德国)

(2)、 巴拿赫 (S. Banach, 1892-1945, 波兰)

(3)、 冯 $\cdot$ 诺依曼 (J. von Neumann, 1903-1957, 美籍匈牙利)

---

3、 几个概念的理解:

(1)、 函数 (function): 数 $\displaystyle \mapsto$ 数. 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{R}\ni x\mapsto x^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 泛函 (functional): 函数 $\displaystyle \mapsto$ 数. 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathscr{R}[a,b]\ni f\mapsto \int_a^b f(x)\mathrm{ d} x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 算子 (operator): 函数 $\displaystyle \mapsto$ 函数. 比如 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{P}[x]\ni f\mapsto f'(x). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 维数的理解:

(1)、 数学分析, 高等代数一般研究 $\displaystyle \mathbb{R}^n$ - 有限维 (finite dimensional).

(2)、 泛函分析一般考虑无限维 (infinite dimensional), 比如 $\displaystyle \mathbb{P}[x]$ 有一组基 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} 1,x,x^2,\cdots,x^n,\cdots. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.1. 度量空间的进一步例子

07.1.1. 度量空间, 离散度量空间

---

1、 回忆 (Recall): 度量空间 (2.1.1度量空间的定义与例子). 设 $\displaystyle X$ 是 一个集合, $\displaystyle d: X\times X\to \mathbb{R}$ 满足

(1)、 正定性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)\gt& 0,\\ d(x,y)=&0\Leftrightarrow x=y, \forall\ x,y\in X; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 对称性 $\displaystyle d(x,y)=d(y,x),\ \forall\ x,y\in X$;

(3)、 三角不等式 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,z)\leq d(x,y)+d(y,z),\ \forall\ x,y,z\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $d$ 是 $\displaystyle X$ 上的一个距离 (distance) 或 度量 (metric), 而 $\displaystyle (X,d)$ 称为距离空间或度量空间.

---

2、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mbox{度量}d\\ \rightarrow&\mbox{球形邻域} U(x;\varepsilon)=\left\{y\in X;\ d(y,x)\lt \varepsilon\right\}\\ \rightarrow&\mbox{开集}O: \forall\ y\in O,\ \exists\ U(y)\in O. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 球形邻域一定是开集!

---

4、 例. 离散 (discrete) 度量空间. 对集合 $\displaystyle X$, 定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\left\{\begin{array}{llllllllllll}1,&x\neq y\\ 0,&x=y\end{array}\right.,\quad \forall\ x,y\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

思考: $U(x;1)=\underline{\ \ \ \ \ \ \ \ \ \ }$, 而 $\left\{x\right\}$ 是开集. 进而

(1)、 $\displaystyle A\subset X\Rightarrow A=\bigcup_{x\in A}\left\{x\right\}$ 是开集. 而离散度量空间中每个子集都是开集.

(2)、 $\displaystyle A\subset X\Rightarrow A^c\subset X\Rightarrow A^c$ 是开集 $\displaystyle \Rightarrow A$ 是闭集, 而离散度量空间中每个子集都是闭集.

(3)、 总结 离散度量空间中的任何子集既开又闭.

07.1.2. 更多的度量空间

---

1、 例. 序列空间 $\displaystyle S$ (sequence). 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} S=\left\{x=\left\{\xi_k\right\}_{k=1}^\infty;\ \xi_k\in\mathbb{R}\mbox{ 或 }\mathbb{C},\ k=1,2,\cdots\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=&\sum_{k=1}^\infty \frac{1}{2^k} \frac{|\xi_k-\eta_k|}{1+|\xi_k-\eta_k|},\\ &x=\left\{\xi_k\right\}_{k=1}^\infty,\ y=\left\{\eta_k\right\}_{k=1}^\infty\in S. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

这里, $\displaystyle \frac{1}{2^k}$ 称为收敛因子.

---

2、 例. 有界函数空间 $\displaystyle B(\varOmega)$ (bounded). 设 $\displaystyle \varOmega$ 是一个集合, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} B(\varOmega)=\left\{x: \ \varOmega\to \mathbb{R}\mbox{ 或 }\mathbb{C};\ \sup_{t\in \varOmega} |x(t)|\lt \infty\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\sup_{t\in \varOmega} |x(t)-y(t)|,\quad \forall\ x,y\in B(\varOmega). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注. $\displaystyle \sup_{t\in \varOmega} |x(t)|\lt \infty$ 是为了保证 $\displaystyle d(x,y)\lt \infty$!

---

3、 例. 可测函数空间 $\mathfrak{M}(X)$ (measurable). 设 $\displaystyle X$ 是可测集, $\displaystyle m(X)\lt \infty$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathfrak{M}(X)=\left\{\begin{array}{c}x: X\to \mathbb{R}\mbox{ 或 }\mathbb{C};\\ x\mbox{ 是 }X\mbox{ 上的可测函数}\end{array}\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=&\int_X \frac{|x(t)-y(t)|}{1+|x(t)-y(t)|}\mathrm{ d} t,\\ &\forall\ x,y\in \mathfrak{M}(X). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注. $m(X)\lt \infty$ 是为了保证 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=&\int_X \frac{|x(t)-y(t)|}{1+|x(t)-y(t)|}\mathrm{ d} t\\ \leq& 1\cdot m(X)\lt \infty! \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 例. $\displaystyle C[a,b]$ 空间 连续函数空间. 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} C[a,b]=\left\{\begin{array}{c}x: \ [a,b]\to \mathbb{R}\mbox{ 或 }\mathbb{C};\\ x\mbox{ 在 }\forall\ t\in [a,b] \mbox{ 处连续}\end{array}\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\max_{a\leq t\leq b} |x(t)-y(t)|,\quad \forall\ x,y\in C[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注. $\displaystyle [a,b]$ 上的连续函数空间 $\displaystyle C[a,b]$ 有界函数空间 $\displaystyle B[a,b]$ 的子空间 (2.1.1度量空间的定义与例子)!

---

5、 例. $\displaystyle \ell^2$ 平方可和序列空间. 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \ell^2=\left\{x=\left\{\xi_k\right\}_{k=1}^\infty ;\ \sum_{k=1}^\infty |\xi_k|^2\lt \infty\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=&\left[\sum_{k=1}^\infty |\xi_k-\eta_k|^2\right]^\frac{1}{2},\\ &x=\left\{\xi_k\right\}_{k=1}^\infty,\ y=\left\{\eta_k\right\}_{k=1}^\infty\in \ell^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注. $\displaystyle \sum_{k=1}^\infty |\xi_k|^2\lt \infty$ 保证了 $\displaystyle d(x,y)\lt \infty$! 还有, 与序列空间 $S$ 相比, 因为 $\displaystyle \ell^2$ 中的序列有个好性质 $\displaystyle \sum_{k=1}^\infty |\xi_k|^2\lt \infty$, 而引入这个度量. 试与 $\mathbb{R}^n$ 比较.

07.2. 度量空间中的极限, 稠密集, 可分空间

07.2.1. 度量空间中的极限

---

1、 回忆2.1.1度量空间的定义与例子 的一些概念.

---

2、 极限: 设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle \left\{x_n\right\}_{n=1}^\infty\subset X,\ x\in X$, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\lim_{m\to\infty}d(x_n,x)=0\\ \Leftrightarrow& \forall\ \varepsilon\gt 0,\ \exists\ N,\ \forall\ n\gt N, d(x_n,x)\lt \varepsilon\\ \Leftrightarrow& \lim_{n\to\infty}d(x_n,x)=0, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\left\{x_n\right\}$ 是收敛点列, $\displaystyle x$ 是 $\displaystyle \left\{x_n\right\}$ 的极限, 记作 $\displaystyle \lim_{n\to\infty}x_n=x$.

---

3、 极限的唯一性: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}x_n=x, \lim_{n\to\infty}x_n=y\Rightarrow x=y. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 收敛点列的有界性: $\lim_{n\to\infty}x_n=x\Rightarrow \left\{x_n\right\}$ 有界.

---

5、 闭集的序列刻画: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{$E$ 是闭集 $\displaystyle \Leftrightarrow$ 若 $\displaystyle E\ni x_n\to x$, 则 $x\in E$.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

注. 啥叫闭集, 就是在极限运算下封闭的集合, 也就是 $E$ 中的序列取个极限, 还要在 $\displaystyle E$ 中! 记得不? 不行就看看2.3.2闭集及其性质

07.2.2. 度量空间中点列收敛的等价刻画

---

1、 $\displaystyle \mathbb{R}^n$ 中点列收敛的等价刻画 ($\mathbb{R}^n$ 中点列收敛等价于按坐标收敛): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x_m=(\xi^m_1,\cdots,\xi^m_n),\ x=(\xi_1,\cdots,\xi_n)\in\mathbb{R}^n, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{m\to\infty}x_m=x\Leftrightarrow \lim_{m\to\infty} \xi^m_k=\xi_k,\ 1\leq k\leq n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle C[a,b]$ 中点列收敛的等价刻画 ($C[a,b]$ 中点列收敛等价于一致收敛): $\displaystyle x_m,x\in C[a,b]$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\lim_{m\to\infty}x_m=x\\ \Leftrightarrow& x_m(t)\mbox{ 在 }[a,b]\mbox{ 上一致收敛于 }x(t). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 序列空间 $S$ 中点列收敛的等价刻画 ($S$ 中点列收敛等价于按坐标收敛): 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x_m=&(\xi^m_1,\cdots,\xi^m_n,\cdots),\\ x=&(\xi_1,\cdots,\xi_n,\cdots)\in S, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{m\to\infty}x_m=x\Leftrightarrow \lim_{m\to\infty}\xi^m_k=\xi_k,\ \forall\ k\in\mathbb{Z}_+. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 可测函数空间 $\displaystyle \mathfrak{M}(X)$ 中点列收敛的等价刻画 ($\mathfrak{M}(X)$ 中点列收敛等价于依测度收敛): 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x_m,x\in \mathfrak{M}(X), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\lim_{m\to\infty}x_m=x\\ \Leftrightarrow &x_m\mbox{ 依测度收敛于 }x, \mbox{ 即 }x_m\Rightarrow x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 总结: 不同空间中收敛概念不一样 (比如依坐标收敛, 一致收敛, 依测度收敛), 但均可引入度量而统一地看成是度量空间中序列的收敛.

07.2.3. 度量空间中的稠密子集, 可分空间

---

1、 稠密 (dense) 子集, 可分 (separable) 空间的概念. 设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle A,D\subset X$.

(1)、 若 $A\subset \bar{D}$, 则称 $D$ 在 $\displaystyle A$ 中稠密. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &x\in A\Rightarrow x\in \bar{D}\left(A\subset \bar{D}\right)\\ \Leftrightarrow& \forall\ \varepsilon\gt 0, U(x;\varepsilon)\cap D\neq \varnothing\left(\mbox{闭包的邻域刻画}\right)\\ \Rightarrow&\mbox{你看, $\displaystyle x$ 的任何邻域都有 $\displaystyle D$ 中的点咯.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

2.2.05闭包的等价刻画

(2)、 若 $\displaystyle \bar{D}=X$, 则称 $D$ 是 $\displaystyle X$ 的稠密子集.

(3)、 若 $\displaystyle X$ 有一个可数稠密子集, 则称 $\displaystyle X$ 是可分空间.

---

2、 例. $\displaystyle \mathbb{R}^n$ 可分.

---

3、 离散度量空间 $\displaystyle X$ 可分 $\displaystyle \Leftrightarrow X$ 可数.

---

4、 例. 有界序列空间 $\displaystyle \ell^\infty$ 不可分: 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \ell^\infty=\left\{x=\left\{\xi_k\right\}_{k=1}^\infty;\begin{array}{c} \xi_k\in\mathbb{R}\mbox{ 或 }\mathbb{C},\\ \sup_{k\gt 1}|\xi_k|\lt +\infty\end{array}\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=&\sup_k |\xi_k-\eta_k|,\\ &x=\left\{\xi_k\right\}_{k=1}^\infty,\ y=\left\{\eta_k\right\}_{k=1}^\infty\in \ell^\infty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle (\ell^\infty,d)$ 不可分.

07.3. 连续映射

07.3.1. 连续映射的定义

---

1、 连续映射的 $\displaystyle \varepsilon-\delta$ 定义: 设 $\displaystyle (X,d), (Y,\rho)$ 是度量空间, $\displaystyle x_0\in X,\ T: \ X\to Y$. 若 $\forall\ \varepsilon\gt 0,\ \exists\ \delta\gt 0,\mathrm{ s.t.}$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left[d(x,x_0)\lt \delta\Rightarrow \rho(Tx,Tx_0)\lt \varepsilon\right]\\ \Leftrightarrow&\left[x\in U(x_0,\delta)\Rightarrow Tx\in U(Tx_0,\varepsilon)\right]\\ \Leftrightarrow&\left[TU(x_0,\delta)\subset U(Tx_0,\varepsilon)\right]\\ \Leftrightarrow&\left[U(x_0,\delta)\subset T^{-1}\underline{U(Tx_0,\varepsilon)}\right], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

[$Tx_0$ 的每个邻域的原像一定包含 $\displaystyle x_0$ 的某个邻域], 则称 $\displaystyle T$ 在 $\displaystyle x_0$ 处连续. 注. 还记得嘛. 1.1集合的表示 讲过: 若 $\displaystyle f: X\to Y$, 则对 $B\subset Y$, 我们有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}\boxed{x\in f^{-1}(B)\Leftrightarrow f(x)\in B.} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 若 $T$ 在 $\displaystyle \forall\ x\in X$ 处连续, 则称 $\displaystyle T$ 在 $\displaystyle X$ 上连续.

07.3.2. 连续映射的三个等价刻画

---

1、 连续映射的序列刻画 (归结原理): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &T\mbox{ 在 }x_0\mbox{ 处连续}\\ \Leftrightarrow& \mbox{ 若 }\lim_{k\to\infty}x_k=x_0,\mbox{ 则 }\lim_{k\to\infty}Tx_k=Tx_0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 连续映射的开集刻画 (开集的原像是开集): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &T: X\to Y\mbox{ 连续}\\ \Leftrightarrow& \mbox{若 }O\mbox{ 是 }Y\mbox{ 中开集, 则 }T^{-1}O\mbox{ 是 }X\mbox{ 中开集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 连续映射的闭集刻画 (闭集的原像是闭集): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &T: X\to Y\mbox{ 连续}\\ \Leftrightarrow& \mbox{若 }F\mbox{ 是 }Y\mbox{ 中闭集, 则 }T^{-1}F\mbox{ 是 }X\mbox{ 中闭集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.4. 柯西 (Cauchy) 点列和完备度量空间

07.4.1. Cauchy 点列

---

1、 Cauchy 点列 设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle \left\{x_n\right\}\subset X$, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ \varepsilon\gt 0,\ \exists\ N,\ \forall\ m,n\gt N,\ d(x_m,x_n)\lt \varepsilon, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\left\{x_n\right\}$ 是 $\displaystyle X$ 中的Cauchy 列.

---

2、 收敛点列是 Cauchy 列: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}x_n=x\Rightarrow \left\{x_n\right\}\mbox{ 是 Cauchy 列}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Cauchy 列是有界列.

---

4、 Cauchy 列如果有一个收敛子列, 则收敛.

---

5、 总结. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{ccccccc} &&\mbox{子列收敛}&&\\ \mbox{收敛列}&&\leftrightarrows&&\mbox{Cauchy 列}\\ &\searrow&&\swarrow&\\ &&\mbox{有界列} \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.4.2. 完备度量空间

---

1、 完备度量空间 (complete metric space): 设 $\displaystyle (X,d)$ 是度量空间, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\left\{x_n\right\}\mbox{ 是 Cauchy 列}\\ \Rightarrow& \exists\ x\in X,\mathrm{ s.t.} \lim_{n\to\infty}x_n=x, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(也即每个 Cauchy 列都收敛, 且极限在 $\displaystyle X$ 中) 则称 $\displaystyle (X,d)$ 是完备度量空间.

---

2、 完备度量空间的子空间: 设 $\displaystyle (X,d)$ 是完备度量空间, $\displaystyle Y\subset X$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (Y,d)\mbox{ 是完备度量空间}\Leftrightarrow Y\mbox{ 是 }X\mbox{ 的闭子集}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.4.3. 完备度量空间的例子

---

1、 $\mathbb{R}^n$ 是完备度量空间.

---

2、 有界序列空间 $\displaystyle \ell^\infty$ 是完备度量空间.

---

3、 收敛序列空间 $\displaystyle C=\left\{x=\left\{\xi_k\right\}_{k=1}^\infty;\ \lim_{k\to\infty}\xi_k\mbox{ 存在}\right\}$ 是完备度量空间.

---

4、 $\displaystyle C[a,b]$ 是完备度量空间.

07.4.4. 不是完备度量空间的例子

---

1、 如何证明一个度量空间 $\displaystyle (X,d)$ 不完备?

(1)、 法一: 存在 $\displaystyle X$ 中的一个 Cauchy 点列 $\displaystyle \left\{x_n\right\}$, 不收敛, 或者收敛但不收敛于 $X$ 中的点.

(2)、 法二: 假设 $\displaystyle (X,d)$ 是完备度量空间 $\displaystyle (\tilde{X},\tilde{d})$ 的子空间, 也即 $\displaystyle X\subset \tilde{X}, d=\tilde{d}|_X$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X\mbox{不完备}\Leftrightarrow X\mbox{作为 $\tilde{X}$ 的子集不是闭的}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle \mathbb{Q}$ 不是完备度量空间.

---

3、 $\displaystyle \mathbb{P}[a,b]$ 不是完备度量空间.

---

4、 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X&=\left\{\begin{array}{c}x: [0,1]\to\mathbb{R};\\ x\mbox{ 在 }\forall\ 0\leq t\leq 1\mbox{ 处连续}\end{array}\right\}, \\ d(x,y)&=\int_0^1 |x(t)-y(t)|\mathrm{ d} t, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle (X,d)$ 不是完备度量空间.

---

5、 注意. 你看:

(1)、 $\displaystyle X=\left\{x: [0,1]\to\mathbb{R};\ x\mbox{在}\forall\ 0\leq t\leq 1\mbox{处连续}\right\}$ 赋以度量 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\max_{0\leq t\leq 1}\left|x(t)-y(t)\right| \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

后, $\displaystyle (X,d)$ 是完备度量空间.

(2)、 $\displaystyle X=\left\{x: [0,1]\to\mathbb{R};\ x\mbox{在}\forall\ 0\leq t\leq 1\mbox{处连续}\right\}$ 赋以度量 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\int_0^1 |x(t)-y(t)|\mathrm{ d} t \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

后, $\displaystyle (X,d)$ 不是完备度量空间.

所以, 讨论完备性一定要看清楚所考虑的度量哦.

07.5. 度量空间的完备化

07.5.1. 序言, 保距映射, 等距同构

---

1、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\mathbb{Q} \mbox{不完备}\left(\mbox{数学危机啦, 引入无理数, 比如 $\displaystyle \sqrt{2}$}\right)\\ \Rightarrow&\mathbb{R}=\mathbb{Q}\cup (\mathbb{R}\backslash \mathbb{Q})\mbox{完备, 且} \mathbb{Q}\mbox{在}\mathbb{R}\mbox{中稠密}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 那么一般的不完备度量空间是否也可成为某一完备度量空间的稠密子空间呢? 本节回答这一问题.

---

3、 保距映射 设 $(X,d)$, $(\tilde{X},\tilde{d})$ 是度量空间, $\displaystyle T: X\to \tilde{X}$ 满足 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \tilde{d}(Tx,Ty)=d(x,y),\quad \forall\ x,y\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle T$ 是保距映射. 例子: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T: &1&\mapsto&\ 3\\ &2&\mapsto&\ 4\\ & & &\ 5 \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 注意. 保距映射一定是单射, 但不一定是满射.

---

5、 等距同构映射: 若 $\displaystyle T: X\to Y$ 是满的保距映射, 则称 $\displaystyle T$ 是从 $\displaystyle X$ 到 $\displaystyle \tilde{X}$ 的等距同构映射, $\displaystyle X$ 和 $\displaystyle \tilde{X}$ 称为等距同构.

---

6、 等距同构的度量空间的一切与距离有关的性质都是一样的, 今后不再区分它们, 视为同一. 正如以前高等代数所说: 线性同构的线性空间不再区分; 同构 (保持线性运算和内积) 的欧氏空间不再区分!

07.5.2. 度量空间的完备化

---

1、 度量空间的完备化: 设 $\displaystyle (X,d)$ 是度量空间, 那么存在唯一的完备度量空间 $\displaystyle (\tilde{X},\tilde{d})$, 使得 $X$ 是 $\displaystyle \tilde{X}$ 的稠密子空间. 这里, 唯一性是在等距同构的意义下!

---

2、 例. $\displaystyle \mathbb{P}[a,b]$ 在距离 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\max_{a\leq t\leq b} |x(t)-y(t)| \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

下的完备化.

---

3、 例. $\displaystyle C[a,b]$ 在距离 $\displaystyle d(x,y)=\int_0^1 |x(t)-y(t)|\mathrm{ d} t$ 下的完备化.

07.6. 压缩映射原理及其应用

07.6.1. 压缩映射原理

---

1、 数学分析做过习题: 设 $\displaystyle \left\{a_n\right\}_{n=0}^\infty$ 是压缩数列, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\exists\ 0\lt \alpha\lt 1,\mathrm{ s.t.}\\ &|a_{n+1}-a_n|\leq \alpha|a_n-a_{n-1}|,\ n\gt 1, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle \left\{a_n\right\}$ 收敛.

---

2、 本节将上述结论推广到完备度量空间.

---

3、 压缩映射 (contraction mapping): 设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle T: X\to X$. 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\exists\ 0\lt \alpha\lt 1,\mathrm{ s.t.}\\ &d(Tx,Ty)\leq \alpha d(x,y),\ \forall\ x,y\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $T$ 是压缩映射. 其一定是连续映射: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\forall\ \varepsilon\gt 0,\exists\ \delta=\frac{\varepsilon{\alpha}}\gt 0,\mathrm{ s.t.}\\ &d(x,y)\lt \delta, d(Tx,Ty)\leq \alpha d(x,y)\lt \alpha \delta=\varepsilon. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 压缩映射的几何意义: $\displaystyle x,y$ 经过 $\displaystyle T$ 映射后, 它们像的距离缩短了, 不超过 $\displaystyle d(x,y)$ 的 $\displaystyle \alpha$ 倍 ($\alpha\lt 1$).

---

5、 压缩映射原理: 设 $\displaystyle X$ 是完备度量空间, $\displaystyle T: X\to X$ 是压缩映射, 那么 $\displaystyle T$ 有且仅有一个不动点 (也即方程 $\displaystyle Tx=x$ 有且仅有一个解).

---

6、 压缩映射原理不仅证明了方程 $\displaystyle Tx=x$ 解的存在性和唯一性, 还提供了求解方法-逐次逼近法: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x_0\in X,\ x_n=T^nx\Rightarrow x=\lim_{n\to\infty}x_n, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

且有误差估计 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x_n,x)\leq \frac{\alpha^n}{1-\alpha}d(x_1,x_0). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.6.2. 压缩映射原理的应用

---

1、 压缩映射原理在分析、微分方程、积分方程、代数方程解的存在性和唯一性定理证明中起了重要作用.

---

2、 压缩映射原理的应用-隐函数存在定理: 设函数 $\displaystyle f(x,y)$ 在带状域 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} a\leq x\leq b,\ -\infty\lt y\lt +\infty \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

中处处连续, 其处处存在关于 $\displaystyle y$ 的偏导数 $\displaystyle f_y'(x,y)$. 如果还存在常数 $m$ 和 $\displaystyle M$, 满足 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} 0\lt m\leq f_y'(x,y)\leq M,\quad m\lt M, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则方程 $f(x,y)=0$ 在区间 $\displaystyle [a,b]$ 上必有唯一的连续函数 $\displaystyle y=\phi(x)$ 作为解: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x,\phi(x))\equiv 0,\ a\leq x\leq b. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 压缩映射原理的应用-常微分方程解的存在性和唯一性定理 (Picard): 设 $\displaystyle f(t,x)$ 是矩形 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} D=\left\{(t,x);\ |t-t_0|\leq a,\ |x-x_0|\leq b\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

上的二元连续函数, 设 $\displaystyle |f(t,x)|\leq M,\ (t,x)\in D$, 又 $f(t,x)$ 在 $\displaystyle D$ 上关于 $\displaystyle x$ 满足 Lipschitz 条件, 即存在常数 $\displaystyle K$, 使对任意的 $(t,x), (t,y)\in D$, 有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} |f(t,x)-f(t,y)|\leq K|x-y|, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

那么方程 $\frac{\mathrm{ d} x}{\mathrm{ d} t}=f(t,x)$ 在区间 $\displaystyle J=[t_0-\beta,t_0+\beta]$ 上有唯一的满足初值条件 $\displaystyle x(t_0)=x_0$ 的连续函数解, 其中 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \beta\lt \min\left\{a,\frac{b}{M},\frac{1}{K}\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

07.7. 线性空间

07.7.1. 线性空间

---

1、 线性空间: 设 $\displaystyle V$ 是一个非空集合, $\displaystyle \mathbb{F}$ 是一个数域 (其中的元素称为数). 若定义了

(1)、 $\displaystyle V$ 中元素的加法运算: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} V\times V&\to V\\ (\alpha,\beta)&\mapsto \alpha+\beta\left(\mbox{称为 $\displaystyle \alpha,\beta$ 的和}\right), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 数与 $\displaystyle V$ 中元素的数乘 (数量乘积) 运算: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{F}\times V&\to V\\ (k,\alpha)&\mapsto k\alpha\left(\mbox{称为 $\displaystyle k,\alpha$ 的数量乘积}\right), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 $\displaystyle \alpha+\beta=\beta+\alpha,\ \forall\ \alpha,\beta\in V$;

(2)、 $(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma),\ \forall\ \alpha,\beta,\gamma\in V$;

(3)、 $X$ 中存在零元素 (记作 $\displaystyle \theta$), 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \alpha+\theta=\alpha,\ \forall\ \alpha\in V; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(4)、 对 $\forall\ \alpha\in V$, 存在 $\alpha$ 的负元素 (记作 $\displaystyle -\alpha$), 使得 $\alpha+(-\alpha)=\theta$;

(5)、 $1\alpha=\alpha,\ \forall\ \alpha \in V$;

(6)、 $k(l\alpha)=(kl)\alpha,\ \forall\ k,l\in \mathbb{R}$ (或 $\displaystyle \mathbb{C}$), $\forall\ \alpha\in V$;

(7)、 $(k+l)\alpha=k\alpha+l\alpha,\ \forall\ k,l\in \mathbb{R}$ (或 $\displaystyle \mathbb{C}$), $\forall\ \alpha\in V$;

(8)、 $k(\alpha+\beta)=k\alpha+k\beta,\ \forall\ k\in \mathbb{R}$ (或 $\displaystyle \mathbb{C}$), $\forall\ \alpha,\beta\in V$,

则称 $V$ 关于上述加法和数乘运算称为线性空间 (或向量空间), $\displaystyle V$ 中的元素称为向量.

---

2、 实线性空间: 若 $\displaystyle \mathbb{F}=\mathbb{R}$, 则称 $V$ 是实线性空间.

---

3、 复线性空间: 若 $\displaystyle \mathbb{F}=\mathbb{C}$, 则称 $V$ 是复线性空间.

---

4、 零元素是唯一的.

---

5、 对 $\displaystyle \forall\ \alpha\in V$, $\alpha$ 的负元素是唯一的.

---

6、 $\displaystyle 0\alpha=\theta,\ \forall\ \alpha\in V$.

---

7、 $k \theta=\theta$, $\forall\ k\in\mathbb{R}$ (或 $\displaystyle \mathbb{C}$).

---

8、 $(-1)\alpha=-\alpha,\ \forall\ \alpha\in V$.

---

9、 线性空间可以定义元素的减法: $\alpha-\beta=\alpha+(-\beta)$.

07.7.2. 线性空间的例子

---

1、 $\mathbb{R}^n$ 是实线性空间.

---

2、 $\displaystyle C[a,b]$ 是线性空间.

---

3、 集合 $\displaystyle \varOmega$ 上的某些函数所成的函数族.

---

4、 $\displaystyle \ell^p\ (p\gt 0)$ 是线性空间.

---

5、 数列空间.

07.7.3. 线性空间的相关概念

---

1、 线性子空间: 设 $\displaystyle V$ 是线性空间, $\displaystyle \varnothing\neq W\subset V$ 对加法和数乘运算封闭, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \alpha,\beta\in W,\ k\in\mathbb{F}\Rightarrow \alpha+\beta,\ k\alpha\in W, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle W$ 是 $\displaystyle V$ 的 (线性) 子空间.

---

2、 $\displaystyle V,\left\{\theta\right\}$ 是 $\displaystyle V$ 的两个子空间, 称为 $\displaystyle V$ 的平凡子空间.

---

3、 若 $\displaystyle W\neq V$, 则称 $W$ 是 $\displaystyle V$ 的真子空间.

---

4、 线性组合: 对 $\displaystyle \left\{\alpha_i\right\}_{i=1}^n\subset V,\ \left\{k_i\right\}_{i=1}^n\subset \mathbb{F}$, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \sum_{i=1}^n k_i\alpha_i \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\alpha_1,\cdots,\alpha_n$ 的线性组合.

---

5、 线性包: 设 $\displaystyle \varnothing \neq M\subset V$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathrm{span} M=\left\{ \sum_{i=1}^n k_i\alpha_i;\begin{array}{c} k_i\in\mathbb{F},\ \alpha_i\in M,\\ i=1,\cdots,n, n\in\mathbb{Z}_+\end{array}\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是包含 $M$ 的最小线性子空间, 称为 $\displaystyle M$ 的线性包.

---

6、 线性相关和线性无关: 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{存在不全为零的数 }k_i,\mathrm{ s.t.} \sum_{i=1}^n k_i\alpha_i=\theta, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle \alpha_1,\cdots,\alpha_n$ 线性相关; 否则称 $\displaystyle \alpha_1,\cdots,\alpha_n$ 线性无关, 也即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\alpha_1,\cdots,\alpha_n\mbox{ 线性无关}\\ \Leftrightarrow& \mbox{若 }\sum_{i=1}^n k_i\alpha_i=\theta, \mbox{ 则 }k_1=\cdots=k_n=0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

7、 注意. 讨论线性相关和线性无关一定要看清所讨论的数域.

---

8、 线性无关子集: 设 $\displaystyle M$ 是线性空间 $\displaystyle V$ 的子集, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 中任意有限个向量都线性无关}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle M$ 是 $\displaystyle X$ 的线性无关子集.

---

9、 两子集线性无关: 设 $\displaystyle M,L$ 是线性空间 $\displaystyle V$ 的两个子集, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 中任何向量与 }L\mbox{ 中任何向量都线性无关}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle M$ 和 $\displaystyle L$ 线性无关.

---

10、 维数: 设 $\displaystyle V$ 是线性空间, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 是 }V\mbox{ 的线性无关子集},\quad \mathrm{span} M=V, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle M$ 的基数 $\displaystyle \overline{\overline{M}}$ 为 $\displaystyle V$ 的维数, 记作 $\displaystyle \dim V$, $M$ 称为 $\displaystyle V$ 的一组基.

(1)、 若 $\displaystyle \overline{\overline{M}}$ 是有限数, 则称 $\displaystyle V$ 是有限维线性空间, 否则称为无限维线性空间.

(2)、 若 $\displaystyle V=\left\{\theta\right\}$, 则称 $V$ 是零维线性空间.

---

11、 任何有限维线性空间的维数不随基的不同而改变.

---

12、 例. $\displaystyle \mathbb{R}^n$ 是 $\displaystyle n$ 维实线性空间.

---

13、 例. $\displaystyle C[a,b]$ 是无限维线性空间.

---

14、 今后线性空间的零向量 $\displaystyle \theta$ 仍记为 $\displaystyle 0$.

07.8. 赋范线性空间和巴拿赫 (Banach) 空间

07.8.1. 赋范线性空间和巴拿赫 (Banach) 空间

---

1、 赋范线性空间 (normed linear space): 设 $X$ 是实 (或复) 线性空间, 若存在 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert \cdot\right\Vert : X&\to\mathbb{R}\\ x&\mapsto\left\Vert x\right\Vert \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 正定性 $\displaystyle \left\Vert x\right\Vert \gt 0,\ \left\Vert x\right\Vert =0\Leftrightarrow x=0,\ \forall\ x\in X$;

(2)、 正齐次性 $\left\Vert \alpha x\right\Vert =|\alpha|\left\Vert x\right\Vert ,\ \forall\ \alpha\in\mathbb{R}$ 或 $\displaystyle \mathbb{C}$, $\forall\ x\in X$;

(3)、 三角不等式 $\left\Vert x+y\right\Vert \leq \left\Vert x\right\Vert +\left\Vert y\right\Vert ,\ \forall\ x,y\in X$,

则称 $\left\Vert x\right\Vert$ 为向量 $\displaystyle x$ 的范数 (norm), $\displaystyle X$ 按范数 $\displaystyle \left\Vert \cdot\right\Vert$ 称为赋范线性空间, 记作 $\displaystyle (X,\left\Vert \cdot\right\Vert )$.

---

2、 依范数收敛 (强收敛): 设 $\left\{x_n\right\}_{n=1}^\infty\subset X,\ x\in X$, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}\left\Vert x_n-x\right\Vert =0, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\left\{x_n\right\}$ 依范数收敛 (强收敛) 于 $\displaystyle x$, 记作 $x_n\to x\ (n\to\infty)$ 或 $\displaystyle \lim_{n\to\infty}x_n=x$.

---

3、 赋范线性空间是度量空间: 设 $(X,\left\Vert \cdot\right\Vert )$ 是赋范线性空间, 则记 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,y)=\left\Vert x-y\right\Vert ,\quad \forall\ x,y\in X \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

后知 $\displaystyle d$ 是 $\displaystyle X$ 上的距离, 而 $\displaystyle (X,d)$ 是度量空间, 且满足

(1)、 $\displaystyle d(\alpha x,0)=|\alpha|d (x,0),\ \forall\ \alpha\in\mathbb{R}$ (或 $\displaystyle \mathbb{C}$), $\forall\ x\in X$;

(2)、 $d(x-y,0)=d(x,y)$, $\forall\ x,y\in X$.

以上两点反映了空间的度量结构与线性结构之间具有某种协调性.

---

4、 Banach 空间: 既然赋范线性空间是度量空间, 就可按照7.4.2完备度量空间 那样考虑其是否是完备的 (Cauchy 列是否一定收敛于空间中某一点). 完备的赋范线性空间称为Banach 空间.

---

5、 范数 $\left\Vert \cdot\right\Vert$ 是赋范线性空间 $\displaystyle X$ 上的连续函数.

07.8.2. Banach 空间的例子

---

1、 $\displaystyle \mathbb{R}^n$ 是 Banach 空间.

---

2、 $\displaystyle \ell^\infty$ 是 Banach 空间.

---

3、 $\displaystyle C[a,b]$ 是 Banach 空间.

---

4、 $\displaystyle \mathscr{L}^p(E)$ 是 Banach 空间.

---

5、 $\displaystyle C[a,b]$ 关于范数 $\displaystyle \left\Vert \cdot\right\Vert _p$ ($p\gt 1$) 不是完备的, 其完备化空间为 $\displaystyle \mathscr{L}^p[a,b]$.

---

6、 Lebesgue 可积函数类 $\mathscr{L}[a,b]$ 是 Riemann 可积函数类 $\displaystyle \mathscr{R}[a,b]$ 在范数 $\displaystyle \left\Vert f\right\Vert _1=\int_{[a,b]} |f(x)|\mathrm{ d} x$ 下的完备化.

---

7、 $\displaystyle \ell^p$ ($p\gt 1$) 是 Banach 空间.

07.8.3. 有限维赋范线性空间

---

1、 有限维线性空间的一个等价范数: 设 $\displaystyle X$ 是 $\displaystyle n$ 维赋范线性空间, $\displaystyle \left\{e_1,\cdots,e_n\right\}$ 是 $\displaystyle X$ 的一组基, 则 $\displaystyle \exists\ M,M'\gt 0,\mathrm{ s.t.}$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &M\left\Vert x\right\Vert \leq \left(\sum_{k=1}^n |\xi_k|^2\right)^\frac{1}{2}\leq M'\left\Vert x\right\Vert ,\\ &\forall\ x=\sum_{k=1}^n \xi_ke_k\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 有限维线性空间的范数均等价: 设在有限维线性空间 $\displaystyle X$ 中定义了两个范数 $\displaystyle \left\Vert \cdot\right\Vert$ 和 $\displaystyle \left\Vert \cdot\right\Vert _1$, 那么 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ M,M'\gt 0,\mathrm{ s.t.} M\left\Vert x\right\Vert \leq \left\Vert x\right\Vert _1\leq M'\left\Vert x\right\Vert . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 赋范线性空间的拓扑同构: 设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (X_1,\left\Vert \cdot\right\Vert _1), (X_2,\left\Vert \cdot\right\Vert _2) \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是两个赋范线性空间, 若存在一一映射 $\phi: \ X_1\to X_2$ 及正数 $\displaystyle c_1,c_2$ 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} c_1\left\Vert \phi(x)\right\Vert _2\leq \left\Vert x\right\Vert _1\leq c_2\left\Vert \phi(x)\right\Vert _2,\quad \forall\ x\in X_1, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle (X_1,\left\Vert \cdot\right\Vert _1)$ 和 $\displaystyle (X_2,\left\Vert \cdot\right\Vert _2)$ 拓扑同构.

---

4、 有限维赋范线性空间拓扑同构: 任何有限维赋范线性空间都和同维数欧氏空间拓扑同构 而是 Banach 空间. 相同维数的有限维赋范线性空间彼此拓扑同构.

08. 有界线性算子和连续线性泛函 (bounded linear operator / functional

08.1. 有界线性算子和连续线性泛函

08.1.1. 线性算子和线性泛函的定义

---

1、 线性算子: 设

(1)、 $\displaystyle X,Y$ 是两个同为 $\displaystyle \mathbb{F}$ ($=\mathbb{R}$ 或 $\displaystyle \mathbb{C}$) 上的线性空间;

(2)、 $\mathscr{D}$ 是 $\displaystyle X$ 的线性子空间, $\displaystyle T: \ \mathscr{D}\to Y$;

(3)、 $T(x+y)=Tx+Ty$, $T(\alpha x)=\alpha Tx$, $\forall\ \alpha\in\mathbb{F},\ x,y\in \mathscr{D}$,

则称

(1)、 $T$ 是 $\displaystyle \mathscr{D}$ 到 $\displaystyle Y$ 的线性算子;

(2)、 $\displaystyle \mathscr{D}$ 称为 $\displaystyle T$ 的定义域, 记作 $\displaystyle \mathscr{D}(T)$;

(3)、 $T\mathscr{D}$ 称为 $\displaystyle T$ 的值域, 记作 $\displaystyle \mathscr{R}(T)$;

(4)、 当 $Y=\mathbb{F}$ ($\mathbb{R}$ 或 $\displaystyle \mathbb{C}$) 时, 称 $T$ 为(实或复) 线性泛函.

---

2、 线性算子的零空间: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathscr{N}(T)=\left\{x\in \mathscr{D}(T);\ Tx=0\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是 $\displaystyle \mathscr{D}$ 的线性子空间.

08.1.2. 线性算子和线性泛函的例子

---

1、 设 $\displaystyle X$ 是线性空间, $\displaystyle \alpha\in\mathbb{F}$, 则有从 $X$ 到 $\displaystyle X$ 中的线性算子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} Tx=\alpha x,\quad \forall\ x\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为相似算子.

(1)、 当 $\displaystyle \alpha=1$ 时, $\displaystyle T$ 称为恒等算子, 记作 $\displaystyle I_X$ 或 $\displaystyle I$;

(2)、 当 $\alpha=0$ 时, $\displaystyle T$ 称为零算子, 记作 $\displaystyle O$.

---

2、 设 $\mathscr{P}[x]$ 为 $\displaystyle [0,1]$ 上多项式全体, 则有从 $\displaystyle \mathscr{P}[0,1]$ 到 $\displaystyle \mathscr{P}[0,1]$ 中的线性算子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (Tx)(t)=\frac{\mathrm{ d} }{\mathrm{ d} t}x(t),\quad \forall\ x\in \mathscr{P}[0,1]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

任意取定 $\displaystyle t_0\in [0,1]$, 则有 $\mathscr{P}[0,1]$ 上的线性泛函 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=x'(t_0),\quad \forall\ x\in \mathscr{P}[0,1]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\displaystyle C[a,b]$ 到 $\displaystyle C[a,b]$ 中的线性算子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (Tx)(t)=\int_a^t x(\tau)\mathrm{ d} \tau,\quad \forall\ x\in C[a,b]; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\displaystyle C[a,b]$ 上的线性泛函 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\int_a^b x(\tau)\mathrm{ d} \tau,\quad \forall\ x\in C[a,b]. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 $\displaystyle C[a,b]$ 到 $\displaystyle C[a,b]$ 中的线性算子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (Tx)(t)=tx(t),\quad \forall\ x\in C[a,b] \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为乘子算子. 在物理及算子谱论中使非常有用的一种算子.

---

5、 $\displaystyle \mathbb{R}^n$ 到 $\displaystyle \mathbb{R}^n$ 中的线性算子 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} Tx=Ax,\quad \forall\ x\in \mathbb{R}^n \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(其中 $\displaystyle A$ 是 $\displaystyle n$ 阶方阵) 称为线性变换. 任取 $\displaystyle (\alpha_1,\cdots,\alpha_n)\in\mathbb{R}^n$, 则有 $\mathbb{R}^n$ 上的线性泛函 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} f(x)=\sum_{\nu=1}^n \alpha_\nu \xi_\nu,\quad \forall\ x=(\xi_1,\cdots,\xi_n)\in\mathbb{R}^n. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(1)、 线性变换 $\displaystyle T$ 完全由矩阵 $\displaystyle A$ 决定.

(2)、 线性泛函 $\displaystyle f$ 完全由 $\displaystyle (\alpha_1,\cdots,\alpha_n)$ 决定.

08.1.3. 有界线性算子和连续线性泛函

---

1、 有界线性算子 设 $\displaystyle X,Y$ 是两个赋范线性空间, $\displaystyle T$ 是 $\displaystyle X$ 的线性子空间 $\displaystyle \mathscr{D}(T)$ 到 $\displaystyle Y$ 中的线性算子, 若

$$\begin{equation}\tag{8.1.2: def bound}\label{8.1.2: def bound}\begin{aligned} \exists\ c\gt 0,\mathrm{ s.t.} \left\Vert Tx\right\Vert \leq c\left\Vert x\right\Vert ,\quad \forall\ x\in \mathscr{D}(T), \end{aligned}\end{equation}$$

则称

(1)、 $\displaystyle T$ 是从 $\displaystyle \mathscr{D}(T)$ 到 $\displaystyle Y$ 中的有界线性算子;

(2)、 若 $\displaystyle \mathscr{D}(T)=X$, 则称 $T$ 是从 $\displaystyle X$ 到 $\displaystyle Y$ 中的有界线性算子, 简称有界算子.

若 \eqref{8.1.2: def bound} 不成立, 也即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ n\in\mathbb{Z}_+,\ \exists\ x_n\in \mathscr{D}(T),\mathrm{ s.t.} \left\Vert Tx_n\right\Vert \gt n\left\Vert x_n\right\Vert , \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle T$ 是无界算子.

---

2、 线性算子的有界性与连续性等价 设 $\displaystyle X,Y$ 是两个赋范线性空间, $\displaystyle T: X\to Y$ 是线性算子, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T\mbox{ 为有界算子}\Leftrightarrow T\mbox{ 是 }X\mbox{ 上的连续算子}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 连续线性泛函的一个充要条件 设 $\displaystyle X$ 是赋范线性空间, $\displaystyle f$ 是 $\displaystyle X$ 上的线性泛函, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &f\mbox{ 是 $\displaystyle X$ 上连续线性泛函}\\ \Leftrightarrow& \mathscr{N}(f)\mbox{ 是 $\displaystyle X$ 的闭子空间}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 算子范数 设 $\displaystyle T$ 是赋范线性空间 $\displaystyle X$ 的子空间 $\displaystyle \mathscr{D}(T)$ 到赋范线性空间 $\displaystyle Y$ 中的线性算子, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert T\right\Vert =\sup_{x\neq 0\atop x\in \mathscr{D}(T)} \frac{\left\Vert Tx\right\Vert }{\left\Vert x\right\Vert } \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为算子 $\displaystyle T$ 在 $\displaystyle \mathscr{D}(T)$ 上的范数.

---

5、 $\displaystyle T$ 是 $\displaystyle \mathscr{D}(T)$ 上的有界线性算子 $\displaystyle \Leftrightarrow \left\Vert T\right\Vert \lt \infty$.

---

6、 算子范数的等价刻画 设 $T$ 是 $\displaystyle \mathscr{D}(T)$ 上的有界线性算子, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert T\right\Vert =\sup_{x\in \mathscr{D}(T)\atop \left\Vert x\right\Vert =1}\left\Vert Tx\right\Vert =\sup_{x\in \mathscr{D}(T)\atop \left\Vert x\right\Vert \leq 1}\left\Vert Tx\right\Vert . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

08.1.4. 有界线性算子和连续线性泛函的例子

---

1、 相似算子的范数 赋范线性空间 $\displaystyle X$ 上的相似算子 $\displaystyle Tx=\alpha x$ 是有界线性算子, 且 $\displaystyle \left\Vert T\right\Vert =|\alpha|$. 特别地, $\left\Vert I_X\right\Vert =1$, $\left\Vert O\right\Vert =0$.

---

2、 积分算子的范数 设 $X=C[0,1]$, $K(t,\tau)$ 是 $\displaystyle [0,1]\times [0,1]$ 上的二元连续函数, 定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} C[0,1]\ni x\mapsto (Tx)(t)=\int_0^t K(t,\tau)x(\tau)\mathrm{ d} \tau, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle T$ 是 $\displaystyle C[0,1]$ 到 $\displaystyle C[0,1]$ 中的线性算子, 称为积分算子, 其中函数 $\displaystyle K(t,\tau)$ 称为 $\displaystyle T$ 的核 (kernel). 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert T\right\Vert =M\stackrel{\rm def}{=} \max_{0\leq t\leq 1} \int_0^1 |K(t,\tau)|\mathrm{ d} \tau, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而 $\displaystyle T$ 是有界算子.

---

3、 不定积分算子的范数 作 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (Tf)(t)=\int_a^t f(\tau)\mathrm{ d} \tau,\quad \forall\ f\in \mathscr{L}^1[a,b], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\displaystyle T: \mathscr{L}^1[a,b]\to \mathscr{L}^1[a,b]$ 是线性算子, 且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert T\right\Vert =b-a, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而 $\displaystyle T$ 是有界线性算子.

---

4、 微分算子是无界算子 微分算子 $\displaystyle (Tx)(t)=\frac{\mathrm{ d}}{\mathrm{ d} t}x(t)$ 是 $\displaystyle \mathscr{P}[0,1]$ 到 $\displaystyle \mathscr{P}[0,1]$ 中的线性算子, 但 $\displaystyle T$ 是无界算子.

08.2. 有界线性算子空间和共轭空间

08.2.1. 有界线性算子全体所成空间

---

1、 记号: 设 $\displaystyle X,Y$ 是赋范线性空间, 记 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathscr{B}(X, Y)&=\left\{T: X\to Y;\ T\mbox{ 是有界线性算子}\right\},\\ \mathscr{B}(X)&=\mathscr{B}(X,X). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle \mathscr{B}(X, Y)$ 是赋范线性空间: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{加法: }&A,B\in \mathscr{B}(X, Y)\\ \Rightarrow& (A+B)(x)=Ax+Bx,\ \forall\ x\in X;\\ \mbox{数乘: }&\alpha\in\mathbb{F},\ A\in \mathscr{B}(X, Y)\\ \Rightarrow& (\alpha A)(x)=\alpha Ax,\quad \forall\ x\in X;\\ \mbox{(算子)范数: }&\left\Vert A\right\Vert =\sup_{x\neq 0}\frac{\left\Vert Ax\right\Vert }{\left\Vert x\right\Vert },\quad \forall\ A\in \mathscr{B}(X, Y). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 当 $\displaystyle Y$ 是 Banach 空间时, $\displaystyle \mathscr{B}(X, Y)$ 也是 Banach 空间.

---

4、 有界线性算子的乘积: 设 $\displaystyle X,Y,Z$ 是赋范线性空间, $\displaystyle A\in \mathscr{B}(X, Y),\ B\in \mathscr{B}(Y,Z)$, 则可定义 $A$ 与 $\displaystyle B$ 的乘积 $\displaystyle BA\in \mathscr{B}(X,Z)$ 如下: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (BA)(x)=B(Ax),\quad \forall\ x\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

且由 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert (BA)x\right\Vert &=\left\Vert B(Ax)\right\Vert \leq \left\Vert B\right\Vert \cdot \left\Vert Ax\right\Vert \\ &\leq \left\Vert B\right\Vert \left\Vert A\right\Vert \left\Vert x\right\Vert ,\quad \forall\ x\in X \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

知 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert BA\right\Vert \leq \left\Vert B\right\Vert \left\Vert A\right\Vert . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 赋范代数和 Banach 代数: 设 $\displaystyle X$ 是赋范线性空间, $\displaystyle X$ 中定义了两个向量的乘积, 且满足 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert xy\right\Vert \leq \left\Vert x\right\Vert \left\Vert y\right\Vert ,\quad \forall\ x\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle X$ 是赋范代数. 当 $\displaystyle X$ 完备时, 称 $\displaystyle X$ 为Banach 代数.

---

6、 $\displaystyle \mathscr{B}(X)$ 是赋范代数; 当 $\displaystyle X$ 是 Banach 空间时, $\displaystyle \mathscr{B}(X)$ 是 Banach 代数.

08.2.2. 共轭空间

---

1、 共轭空间: 设 $\displaystyle X$ 是赋范线性空间, 称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X'=\left\{f: X\to\mathbb{F};\ f\mbox{ 是连续线性泛函}\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle X$ 的共轭空间.

---

2、 共轭空间是 Banach 空间: 任何赋范线性空间的共轭空间都是 Banach 空间.

---

3、 赋范线性空间的同构.

(1)、 设 $\displaystyle X,Y$ 是两个赋范线性空间, $\displaystyle T: \ X\to Y$ 是线性算子, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert Tx\right\Vert =\left\Vert x\right\Vert ,\quad \forall\ x\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle T$ 是 $\displaystyle X$ 到 $\displaystyle Y$ 中的保距算子.

(2)、 若 $\displaystyle T$ 又是映射到 $\displaystyle Y$ 上的 (即 $\displaystyle T$ 是满射), 则称 $\displaystyle T$ 是同构映射, 此时称 $\displaystyle X,Y$ 同构.

---

4、 保距算子是单射.

---

5、 同构映射保持线性运算及范数不变, 而同构的赋范线性空间 $\displaystyle X,Y$ 看成一样, 不加以区分, 记作 $\displaystyle X=Y$.

---

6、 例. $(\ell^1)'=\ell^\infty$.

---

7、 例. $(\ell^p)'=\ell^q,\quad 1\lt p\lt \infty,\ \frac{1}{p}+\frac{1}{q}=1$.

08.3. 有限秩算子

08.3.1. 有限秩算子

---

1、 本节讨论与矩阵最接近的算子: 有限秩算子.

---

2、 有限秩 (finite rank) 算子的定义: 设

(1)、 $X,Y$ 是 Banach 空间,

(2)、 $\displaystyle T\in\mathscr{B}(X, Y)$,

若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \dim \mathscr{R}(T)\lt \infty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $T$ 是有限秩的? 为啥这么称呼? 并记

(1)、 $\displaystyle \mathscr{F}(X,Y)$ 是 $\displaystyle \mathscr{B}(X,Y)$ 中有限秩算子全体.

(2)、 $\displaystyle \mathscr{F}(X)=\mathscr{F}(X,X)$.

---

3、 例. 设

(1)、 $X,Y$ 是 Banach 空间;

(2)、 $\displaystyle \left\{y_1,\cdots,y_n\right\}$ 是 $\displaystyle Y$ 中一组线性无关的向量;

(3)、 $\displaystyle f_1,\cdots,f_n\in X'$,

定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} Tx=\sum_{k=1}^n f_k(x)y_k,\quad \forall\ x\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则

(1)、 $T$ 是线性算子.

(2)、 $\displaystyle T\in \mathscr{B}(X,Y)$.

(3)、 $T\in\mathscr{F}(X,Y)$. (且 $\mathscr{F}(X,Y)$ 中的所有有限秩算子都具有这种形式, 参见张恭庆林源渠泛函分析讲义第 209 页定理 4.1.10.)

08.3.2. 有限秩算子全体是 Banach 代数的一个理想

---

1、 群 (group) 的定义. 若非空集合 $\displaystyle G$ 上定义了一个二元函数 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cccc} \circ: &G\times G&\to&G\\ &(a,b)&\mapsto&a\circ b \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 结合律: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (a\circ b)\circ c=a\circ (b\circ c),\quad \forall\ a,b,c\in G; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(2)、 存在幺元: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ e\in G,\mathrm{ s.t.} e\circ a=a\circ e=a,\quad \forall\ a\in G; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 存在逆元: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ a\in G, \exists\ b\in G,\mathrm{ s.t.} a\circ b=b\circ a=e, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle (G,\circ)$ 为群, 简记为 $\displaystyle G$. 再若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} a\circ b=b\circ a, \quad \forall\ a,b\in G, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $G$ 为交换群或 Abel 群.

---

2、 环 (ring) 的定义. 若非空集合 $\displaystyle R$ 上定义了两个二元运算 $\displaystyle +,\cdot$ (分别称为加法, 乘法) $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cccc} +: &G\times G&\to&G\\ &(a,b)&\mapsto&a+ b,\\ \cdot: &G\times G&\to&G\\ &(a,b)&\mapsto&a\cdot b, \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 $\displaystyle (R,+)$ 是 Abel 群;

(2)、 乘法结合律: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (a\cdot b)\cdot c=a\cdot (b\cdot c),\quad \forall\ a,b,c\in R; \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

(3)、 分配律: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} (a+b)\cdot c&=a\cdot b+b\cdot c,\\ c\cdot(a+b)&=c\cdot a+c\cdot b,\quad \forall\ a,b,c\in R, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle (R,+,\cdot)$ 为一个环, 简记为 $\displaystyle R$.

---

3、 理想 (ideal) 的定义. 设

(1)、 $(R,+,\cdot)$ 是一个环;

(2)、 $\displaystyle I$ 是 $\displaystyle R$ 的一个加法子群;

(3)、 $\displaystyle \forall\ r\in R, rI\subset I, Ir\subset I$,

则称 $I$ 是 $\displaystyle R$ 的一个双边理想, 简称理想.

---

4、 $\displaystyle \mathscr{F}(X)$ 是 $\displaystyle \mathscr{B}(X)$ 的一个理想. 设

(1)、 $\displaystyle X$ 是 Banach 空间,

(2)、 $\displaystyle S,T\in \mathscr{F}(X)$,

(3)、 $A\in \mathscr{B}(X)$,

则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} S+T\in \mathscr{F}(X), AS,SA\in \mathscr{F}(X). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而 $\mathscr{F}(X)$ 是 $\displaystyle \mathscr{B}(X)$ 的一个理想.

08.3.3. 商空间

---

1、 商空间 (quotient space) 的定义. 设

(1)、 $\displaystyle X$ 是赋范线性空间,

(2)、 $\displaystyle V$ 是 $\displaystyle X$ 的闭子空间.

定义 $\displaystyle X$ 上的一个等价关系 (equivalence relation): $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\sim y\stackrel{\rm def}{\Leftrightarrow} x-y\in V. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称

(1)、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \ [x]=\left\{y\in X; y\sim x\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle x$ 的等价类 (equivalent class),

(2)、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X/V=\left\{[x]; x\in X\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle X$ (以 $\displaystyle V$ 为模) 的商空间.

---

2、 $\displaystyle X/V$ 是线性空间: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \ [x]+[y]&=[x+y],\\ \ \alpha [x]&=[\alpha x], \quad \forall\ \mbox{数}\alpha, x,y\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 $\displaystyle X/V$ 是赋范线性空间: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert [x]\right\Vert =\inf\left\{\left\Vert y\right\Vert ; y\sim x\right\},\quad \forall\ x\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 $\displaystyle X/V$ 是 Banach 空间.

08.3.4. 商空间的例子

---

1、 例. 设 $\displaystyle X=C[0,1]$, 赋以范数 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert f\right\Vert =\max_{[0,1]}|f|,\quad \forall\ f\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

令 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} V=\left\{f\in X; f(1)=0\right\}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $V$ 是 $\displaystyle X$ 的闭子空间, 且 $\displaystyle X/V$ 与 $\displaystyle \mathbb{C}$ 等距同构.

08.3.5. 通过商空间将映射化为单射来处理

---

1、 设

(1)、 $\displaystyle X,Y$ 是赋范线性空间,

(2)、 $\displaystyle T\in \mathscr{B}(X,Y)$.

则可定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cccc} \hat T: &X/\mathscr{N}(T)&\to&Y\\ &[x]&\mapsto&Tx. \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

且 $\hat T$ 是单射, $\displaystyle \left\Vert \hat T\right\Vert =\left\Vert T\right\Vert$.

08.3.6. 闭值域的一个充分条件

---

1、 设

(1)、 $X$ 是 Banach 空间, $\displaystyle Y$ 是赋范线性空间,

(2)、 $\displaystyle T\in \mathscr{B}(X,Y)$.

若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ \gamma\gt 0,\mathrm{ s.t.} \forall\ x\in X, \left\Vert Tx\right\Vert \gt \gamma\left\Vert x\right\Vert , \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $\mathscr{R}(T)$ 是闭的.

08.3.7. 恒等算子的有限秩扰动不改变值域的闭性

---

1、 设

(1)、 $\displaystyle X$ 是 Banach 空间,

(2)、 $\displaystyle T\in \mathscr{F}(X)$,

则 $\mathscr{R}(I+T)$ 是 $\displaystyle X$ 中的闭子空间.

---

2、 最后, 我们说明一下. 矩阵 $\displaystyle \to$ 有限秩算子 $\displaystyle \to$ 紧算子. 不断推广.

09. 内积空间和希尔伯特空间 (inner product / Hilbert space

09.0. 引论

---

1、 $\displaystyle \mathbb{R}^n$ 中,

(1)、 向量有长度 $\displaystyle \left\Vert x\right\Vert =\sqrt{\sum_{k=1}^n \xi_k^2},\ x=(\xi_1,\cdots,\xi_n)$,

(2)、 两向量之间有夹角 $\alpha: \ \cos\alpha=\frac{x\cdot y}{\left\Vert x\right\Vert \cdot \left\Vert y\right\Vert }$.

---

2、 第 7 章, 我们已经把 $\mathbb{R}^n$ 中向量的长度 $\displaystyle \to$ 赋范线性空间中向量的范数.

---

3、 本章, 我们把 $\displaystyle \mathbb{R}^n$ 中两向量的内积 $\displaystyle \to$ 内积空间中两向量的内积.

09.1. 内积空间的基本概念

09.1.1. 内积空间的定义

---

1、 内积 (inner product) 空间: 设 $\displaystyle X$ 是域 $\displaystyle \mathbb{F}$ ($=\mathbb{R}$ 或 $\displaystyle \mathbb{C}$) 上的线性空间, 若存在 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cccc} \left\lt \cdot,\cdot\right\gt : &X\times X&\to& \mathbb{F}\\ &(x,y)&\mapsto& \left\lt x,y\right\gt \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

满足

(1)、 正定性 $\left\lt x,x\right\gt \gt 0,\ \forall\ x\in X$; $\left\lt x,x\right\gt =0\Leftrightarrow x=0$;

(2)、 关于第一个变元线性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt \alpha x+\beta y,z\right\gt =\alpha \left\lt x,z\right\gt +\beta\left\lt y,z\right\gt , \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\forall\ x,y,z\in X,\ \forall\ \alpha,\beta\in \mathbb{F}$;

(3)、 共轭对称性 $\left\lt x,y\right\gt =\overline{\left\lt y,x\right\gt }$, $\forall\ x,y\in X$,

则称 $\left\lt x,y\right\gt$ 为 $\displaystyle x$ 与 $\displaystyle y$ 的内积; $\displaystyle X$ 称为内积空间, 记作 $\displaystyle (X,\left\lt \cdot,\cdot\right\gt )$.

---

2、 注意. 内积空间中, 内积关于第二个变元共轭线性 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt x,\alpha y+\beta z\right\gt =&\overline{\alpha} \left\lt x,y\right\gt +\overline{\beta} \left\lt x,z\right\gt ,\\ &\forall\ x,y,z\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

09.1.2. 内积空间与赋范线性空间的联系

---

1、 内积空间一定是赋范线性空间. 设 $(X,\left\lt \cdot,\cdot\right\gt )$ 是内积空间, 定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert x\right\Vert =\sqrt{\left\lt x,x\right\gt },\quad \forall\ x\in X \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

后, $\displaystyle (X,\left\lt \cdot,\cdot\right\gt )$ 成为赋范线性空间.

(1)、 $\displaystyle \left\Vert x\right\Vert \gt 0,\ \forall\ x\in X$; $\left\Vert x\right\Vert =0\Leftrightarrow \left\lt x,x\right\gt =0\Leftrightarrow x=0$;

(2)、 $\left\Vert \alpha x\right\Vert =|\alpha| \left\Vert x\right\Vert ,\ \forall\ \alpha\in\mathbb{F},\ \forall\ x\in X$;

(3)、 $\left\Vert x+y\right\Vert \leq \left\Vert x\right\Vert +\left\Vert y\right\Vert ,\ \forall\ x,y\in X$.

---

2、 Hilbert 空间: 完备的内积空间称为 Hilbert 空间. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cc} \mbox{内积空间}&\mbox{是赋范线性空间},\\ \mbox{Hilbert 空间 }&\mbox{是 Banach 空间}\\ \uparrow&\uparrow\\ \mbox{(完备的内积空间)}&\mbox{ (完备的赋范线性空间)}. \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 内积是 $X\times X$ 上的连续函数.

---

4、 赋范线性空间 $\displaystyle (X,\left\Vert \cdot\right\Vert )$ 当且仅当满足平行四边形公式 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert x+y\right\Vert ^2+\left\Vert x-y\right\Vert ^2=&2\left(\left\Vert x\right\Vert ^2+\left\Vert y\right\Vert ^2\right),\\ &\forall\ x,y\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

才可通过极化恒等式 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathbb{F}=\mathbb{C}\Rightarrow \left\lt x,y\right\gt =&\frac{1}{4}\sum_{k=0}^3 \mathrm{ i}^k\left\Vert x+\mathrm{ i}^k y\right\Vert ^2,\\ &\forall\ x,y\in X\\ \mathbb{F}=\mathbb{R}\Rightarrow \left\lt x,y\right\gt =&\frac{1}{4} \left(\left\Vert x+y\right\Vert ^2-\left\Vert x-y\right\Vert ^2\right),\\ &\forall\ x,y\in X \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

定义内积, 而成为内积空间. (参见书第 180 页题 5.)

09.1.3. 内积空间的例子

---

1、 $\displaystyle \mathscr{L}^2(E)$ 是 Hilbert 空间.

---

2、 $\displaystyle \ell^2$ 是 Hilbert 空间.

---

3、 $\displaystyle n$ 阶实方阵全体上引入内积成为 Hilbert 空间.

---

4、 给定一个正定矩阵, 在 $\displaystyle \mathbb{R}^n$ 中引入新的内积成为 Hilbert 空间.

---

5、 当 $\displaystyle p\neq 2$ 时, $\displaystyle \ell^p$ 不是内积空间.

---

6、 $\displaystyle C[a,b]$ 按范数 $\displaystyle \left\Vert x\right\Vert =\max_{a\leq t\leq b}|x(t)|$ 不是内积空间.

09.2. 投影定理

09.2.1. 引言

---

1、 我们知道平面中有点 $\displaystyle x$ 到直线 $\displaystyle L$ 的距离概念, 并且点 $\displaystyle x$ 到垂足 $\displaystyle y$ 所在直线与 $\displaystyle L$ 垂直.

---

2、 本节将上述内容推广到 Hilbert 空间中去.

---

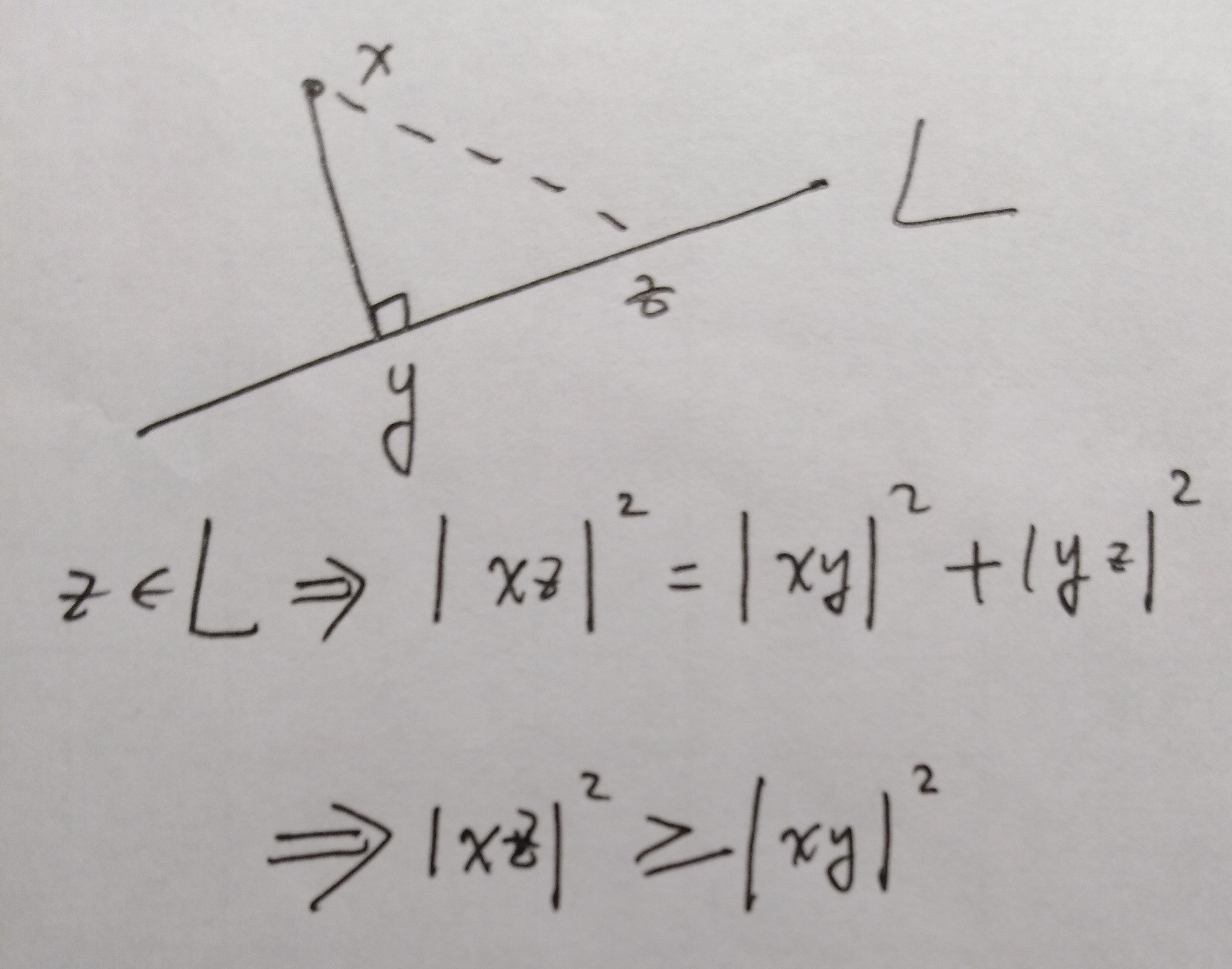
3、 度量空间中点到集合的距离: 设 $\displaystyle (X,d)$ 是度量空间, $\displaystyle x\in X$, $M\subset X$, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} d(x,M)\stackrel{\rm def}{=} \inf_{y\in M} d(x,y) \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $x$ 到 $\displaystyle M$ 的距离.

---

4、 思考.

(1)、 是否$\exists\ y_0\in M,\mathrm{ s.t.} d(x,M)=d(x,y_0)$, 即 $\displaystyle x$ 到 $\displaystyle M$ 的距离是否可以达到?

(2)、 若达到, 是否唯一?

09.2.2. 极小化向量定理

---

1、 线性空间中的线段: 设 $\displaystyle X$ 是线性空间, $\displaystyle x,y\in X$, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \ [x,y]\stackrel{\rm def}{=} \left\{z=(1-\lambda)x+\lambda y;\ 0\leq \lambda \leq 1\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为联结 $x,y$ 的线段.

---

2、 线性空间中的凸集: 设 $\displaystyle X$ 是线性空间, $\displaystyle M\subset X$, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x,y\in M\Rightarrow [x,y]\in M, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $M$ 是 $\displaystyle X$ 中凸集.

---

3、 极小化向量定理: 设 $\displaystyle X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 中非空凸集, 并且按 $\displaystyle X$ 中由内积导出的距离完备, 那么对每个 $\displaystyle x\in X$, 存在唯一的 $y\in M$, 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert x-y\right\Vert =d(x,M). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 极小化向量定理在完备子空间的情形: 设 $X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 的一完备子空间, 则对每个 $\displaystyle x\in X$, 存在唯一的 $y\in M$, 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert x-y\right\Vert =d(x,M). \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 极小化向量定理是内积空间的一个基本定理, 它在微分方程, 现代控制论和逼近论中有重要应用.

09.2.3. 内积空间中的正交, 极小化向量的性质

---

1、 内积空间中的正交: 设 $X$ 是内积空间, $\displaystyle x,y\in X$, $A, B\subset X$,

(1)、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt x,y\right\gt =0, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $x,y$ 互相垂直或正交, 记作 $\displaystyle x\perp y$;

(2)、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt x,y\right\gt =0,\quad \forall\ x\in B, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $x$ 与 $\displaystyle B$ 正交, 记作 $\displaystyle x\perp B$;

(3)、 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt x,y\right\gt =0,\quad \forall\ x\in A,\ \forall\ y\in B, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $A,B$ 正交, 记作 $\displaystyle A\perp B$.

(4)、 勾股定理: 设 $X$ 是内积空间, $\displaystyle x,y\in X$, $x\perp y$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert x+y\right\Vert ^2=\left\Vert x\right\Vert ^2+\left\Vert y\right\Vert ^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 内积空间中极小化向量的性质: 设 $X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 的线性空间, $\displaystyle x\in X$. 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ y\in M,\mathrm{ s.t.} \left\Vert x-y\right\Vert =d(x,M), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则 $(x-y)\perp M$.

09.2.4. 线性空间中的代数补子空间 (直和)

---

1、 代数补子空间: 设 $X$ 是线性空间, $\displaystyle Y,Z$ 是 $\displaystyle X$ 的两个子空间, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ x\in X,\ \exists\ |\ y\in Y,\ z\in Z,\mathrm{ s.t.} x=y+z, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称

(1)、 $\displaystyle X$ 是 $\displaystyle Y$ 和 $\displaystyle Z$ 的直和, 记作 $\displaystyle X=Y\dot +Z$;

(2)、 $Y$ 和 $\displaystyle Z$ 是 $\displaystyle X$ 的一对互补子空间;

(3)、 $\displaystyle Z$ 是 $\displaystyle Y$ 的代数补子空间, $\displaystyle Y$ 是 $\displaystyle Z$ 的代数补子空间.

---

2、 例. $\displaystyle X=\mathbb{R}^2$, $Y$ 是一过原点的直线, 则任一过原点但异于 $\displaystyle Y$ 的直线 $\displaystyle Z$ 都是 $\displaystyle Y$ 的代数补子空间.

---

3、 设 $\displaystyle X$ 是 线性空间, $\displaystyle Y,Z$ 是 $\displaystyle X$ 的两个子空间, 且 $\displaystyle X=Y\dot +Z$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left.\begin{array}{rrrr} 0\neq y\in Y\\ 0\neq z\in Z \end{array}\right\}\Rightarrow y,z\mbox{ 线性无关}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

09.2.5. 内积空间中的正交补子空间

---

1、 正交补子空间: 设 $X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 的子集, 则称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M^\perp=\left\{x\in X;\ x\perp M\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle M$ 在 $\displaystyle X$ 中的正交补. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \color{red}x\in M^\perp\Leftrightarrow x\perp M. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle M^\perp$ 是 $\displaystyle X$ 的闭子空间.

---

3、 若 $\displaystyle M$ 是 $\displaystyle X$ 的线性子空间, 则 $\displaystyle M\cap M^\perp=\left\{0\right\}$.

---

4、 $M^\perp=\overline{M}^\perp$.

---

5、 $M^\perp =(\mathrm{span} M)^\perp =(\overline{\mathrm{span} M})^\perp$.

---

6、 记 $M^{\perp\perp}=(M^\perp)^\perp$, 则 $M\subset M^{\perp\perp}$. ($M$ 包含于其正交补的正交补)

09.2.6. Hilbert 空间中的正交分解

---

1、 投影定理: 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle Y$ 是 $\displaystyle X$ 的闭子空间, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X=Y\dot +Y^\perp. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 正交和正交投影: 设 $\displaystyle X$ 是内积空间, $\displaystyle Y,Z$ 是 $\displaystyle X$ 的两个子空间, 若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X=Y\dot +Z,\quad Y\perp Z, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle X$ 是 $\displaystyle Y$ 与 $\displaystyle Z$ 的正交和, 记作 $\displaystyle X=Y\oplus Z$; 而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \forall\ x\in X,\ \exists\ |\ y\in Y,\ \exists\ |\ z\in Z,\mathrm{ s.t.} x=y+z, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

记作 $x=y\oplus z$. 定义 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} P: \ X\ni x\mapsto y\in Y \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $X$ 到 $\displaystyle Y$ 上的映射, 称为投影算子, 其具有性质:

(1)、 $\displaystyle P$ 是从 $\displaystyle X$ 到 $\displaystyle Y$ 的有界线性算子, 且当 $\displaystyle Y\neq \left\{0\right\}$ 时, $\displaystyle \left\Vert P\right\Vert =1$;

(2)、 $PX=Y$, $PY=Y$, $PY^\perp=\left\{0\right\}$;

(3)、 $P^2=P$, 其中 $P^2=P\cdot P$ 是算子的乘积.

---

3、 投影定理的一个新描述. 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle Y$ 是 $\displaystyle X$ 的闭子空间, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} X=Y\oplus Y^\perp. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 正交补的正交补: 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle Y$ 是 $\displaystyle X$ 的闭子空间, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} Y=Y^{\perp\perp}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 内积空间中子集的线性包稠密的充要条件: 设 $\displaystyle M$ 是 Hilbert 空间 $\displaystyle X$ 中的非空子集, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\mathrm{span} M}=X\Leftrightarrow M^\perp=\left\{0\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

09.3. 希尔伯特空间中的规范正交基

09.3.1. 引论

---

1、 $\displaystyle \mathbb{R}^n$ 中有标准正交基 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} e_i=(\underbrace{0,\cdots,0,1}_i,0,\cdots,0),\ i=1,\cdots,n, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in\mathbb{R}^n\Rightarrow x=\sum_{i=1}^n \left\lt x,e_i\right\gt e_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 对 $\displaystyle \mathbb{R}^n$ 中 $\displaystyle m(m\leq n)$ 个线性无关的向量 $\displaystyle x_1,\cdots,x_m$, 我们可通过 Gram-Schmidt 过程而标准正交化: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} y_1&=\frac{x_1}{\left\Vert x_1\right\Vert },\\ y_2&=\frac{x_2-\left\lt x_2,y_1\right\gt y_1}{\left\Vert x_2-\left\lt x_2,y_1\right\gt y_1\right\Vert },\\ \cdot&=\cdots,\\ y_m&=\frac{\boxed{\begin{array}{c}x_m-\left\lt x_m,y_1\right\gt y_1-\cdots\\-\left\lt x_m,y_{m-1}\right\gt y_{m-1}\end{array}}} {\left\Vert \boxed{\begin{array}{c}x_m-\left\lt x_m,y_1\right\gt y_1-\cdots\\-\left\lt x_m,y_{m-1}\right\gt y_{m-1}\end{array}}\right\Vert }. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 本节将上述内容推广到内积空间中去.

09.3.2. 正交系

---

1、 正交系: 设 $X$ 是内积空间, $\displaystyle 0\not \in M\subset X$.

(1)、 若 $M$ 中向量两两正交, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x,y\in M\Rightarrow x\perp y \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle M$ 是 $\displaystyle X$ 的正交系;

(2)、 又若 $\displaystyle M$ 中向量的范数都是 $\displaystyle 1$, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in M\Rightarrow \left\Vert x\right\Vert =1, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $M$ 是 $\displaystyle X$ 的规范正交系;

(3)、 再若 $\displaystyle M$ 的线性包在 $\displaystyle X$ 中稠密, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \overline{\mathrm{span} M}=X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $\displaystyle M$ 是 $\displaystyle X$ 的完全规范正交系.

---

2、 例. $\displaystyle \mathbb{R}^n$ 中的规范正交系. $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} e_i=(\underbrace{0,\cdots,0,1}_i,0,\cdots,0),\ i=1,\cdots,n \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

是 $\displaystyle \mathbb{R}^n$ 的规范正交系.

---

3、 例. $\displaystyle L^2[0,2\pi]$ 中的规范正交系. 在 $\displaystyle L^2[0,2\pi]$ 中, 定义内积为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt f,g\right\gt =\frac{1}{\pi}\int_0^{2\pi} f(x)g(x)\mathrm{ d} x,\quad \forall\ f,g\in L^2[0,2\pi], \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则三角函数系 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \frac{1}{\sqrt{2}},\cos x,\sin x,\cdots,\cos nx,\sin nx,\cdots \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle L^2[0,2\pi]$ 中的规范正交系.

---

4、 内积空间中规范正交系是正交函数系的推广.

---

5、 设 $\displaystyle M$ 是内积空间 $\displaystyle X$ 中的正交系, 则有勾股定理: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{x_i\right\}_{i=1}^n\subset M\Rightarrow \left\Vert \sum_{i=1}^n x_i\right\Vert ^2=\sum_{i=1}^n \left\Vert x_i\right\Vert ^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

6、 设 $\displaystyle M$ 是内积空间 $\displaystyle X$ 中的正交系, 则 $\displaystyle M$ 是 $\displaystyle X$ 的线性无关子集.

09.3.3. 内积空间中的 Fourier 系数

---

1、 内积空间中的 Fourier 系数: 设 $\displaystyle X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 中规范正交系, 则称数集 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\{\left\lt x,e\right\gt ;\ e\in M\right\} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为向量 $\displaystyle x$ 关于规范正交系 $\displaystyle M$ 的 Fourier 系数集, 而称 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt x,e\right\gt \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

为 $\displaystyle x$ 关于 $\displaystyle e$ 的 Fourier 系数.

---

2、 例. $\displaystyle L^2[0,2\pi]$ 中向量关于三角函数系的 Fourier 系数.

---

3、 内积空间 $\displaystyle X$ 中向量 $\displaystyle x$ 关于规范正交系 $\displaystyle M$ 的 Fourier 系数是数学分析中 Fourier 系数的推广.

---

4、 几何意义: 用规范正交系的线性组合去逼近 $\displaystyle x$, 则 $x$ 的 Fourier 系数给出了最佳逼近元: 设 $\displaystyle X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 的规范正交系, 任取 $\displaystyle M$ 中有限个向量 $\displaystyle e_1,\cdots,e_n$, 那么有

$$\begin{equation}\tag{9.3: apprI}\label{9.3: apprI}\begin{aligned} &\left\Vert x-\sum_{i=1}^n \left\lt x,e_i\right\gt e_i\right\Vert ^2\\ =&\left\Vert x\right\Vert ^2 -\sum_{i=1}^n \left|\left\lt x,e_i\right\gt \right|^2\gt 0, \end{aligned}\end{equation}$$

$$\begin{equation}\tag{9.3: apprII}\label{9.3: apprII}\begin{aligned} &\left\Vert x-\sum_{i=1}^n \alpha_ie_i\right\Vert ^2\\ \gt& \left\Vert x-\sum_{i=1}^n \left\lt x,e_i\right\gt e_i\right\Vert ^2,\quad \forall\ \alpha_1,\cdots,\alpha_n\in\mathbb{F}. \end{aligned}\end{equation}$$

---

5、 注意. 由 Fourier 系数构造的向量是正交投影.

09.3.4. 内积空间中的 Bessel 不等式、Parseval 等式、Riemann-Lebesgue 引理

---

1、 Bessel 不等式: 设 $\left\{e_k\right\}$ 是内积空间 $\displaystyle X$ 的有限或可数规范正交系, 那么

$$\begin{equation}\tag{9.3: Bessel inequality: ineq}\label{9.3: Bessel inequality: ineq}\begin{aligned} x\in X\Rightarrow \sum_{i=1}^{n\mbox{或}\infty} |\left\lt x,e_i\right\gt |^2\leq \left\Vert x\right\Vert ^2. \end{aligned}\end{equation}$$

---

2、 Parseval 等式. 若 \eqref{9.3: Bessel inequality: ineq} 中等号成立, 则称其为 Parseval 等式.

---

3、 Riemann-Lebesgue 引理: 设 $\displaystyle \left\{e_k\right\}$ 是 $\displaystyle X$ 中可数规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in X\Rightarrow \lim_{n\to\infty} \left\lt x,e_n\right\gt =0. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 Bessel 不等式的一般形式: 设 $\displaystyle \left\{e_\lambda\right\}_{\lambda \in \varLambda}$ 是内积空间 $\displaystyle X$ 中的规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in X\Rightarrow \sum_{\lambda\in\varLambda} |\left\lt x,e_\lambda\right\gt |^2\leq \left\Vert x\right\Vert ^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

证明中将指出: 上述和式中只有有限或可数个不为 $\displaystyle 0$.

09.3.5. 抽象空间中的级数论

---

1、 赋范线性空间中的级数: 设 $X$ 是赋范线性空间, $\displaystyle \left\{x_i\right\}_{i=1}^\infty\subset X$, 其前 $n$ 项和为 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} S_n=\sum_{i=1}^n x_i. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

若 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ x\in X,\mathrm{ s.t.} \lim_{n\to\infty}S_n=x, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称级数 $\displaystyle \sum_{n=1}^\infty x_n$ 收敛, 且称 $\displaystyle x$ 为该级数的和, 记作 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \sum_{i=1}^\infty x_i=x. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Hilbert 空间中的级数: 设 $\displaystyle \left\{e_k\right\}$ 为 Hilbert 空间 $\displaystyle X$ 中可数规范正交系, 那么

(1)、 级数 $\displaystyle \sum_{i=1}^\infty \alpha_ie_i$ 收敛 $\displaystyle \Leftrightarrow \sum_{i=1}^\infty |\alpha_i|^2$ 收敛;

(2)、 若 $\displaystyle x=\sum_{i=1}^\infty \alpha_ie_i$, 则 $\alpha_i=\left\lt x,e_i\right\gt$, 而 $x=\sum_{i=1}^\infty \left\lt x,e_i\right\gt e_i$;

(3)、 对 $\forall\ x\in X$, 级数 $\sum_{i=1}^\infty \left(x,e_i\right)e_i$ 收敛.

09.3.6. 内积空间中的规范正交系的完全性

---

1、 内积空间中规范正交系完全的充要条件: 设 $\displaystyle X$ 是内积空间, $\displaystyle M$ 是 $\displaystyle X$ 的规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 完全}\Leftrightarrow M^\perp=\left\{0\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 Hilbert 空间中规范正交系完全的充要条件: 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle M$ 是 $\displaystyle X$ 的规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 完全}\Leftrightarrow \forall\ x\in X,\ \mbox{ Parseval 等式成立: } \left\Vert x\right\Vert ^2=\sum_{e\in M}|\left\lt x,e\right\gt |^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 Hilbert 空间中的 Fourier 展开式. 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle M$ 是 $\displaystyle X$ 的完全规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} x\in X\Rightarrow x=\sum_{e\in M}\left\lt x,e\right\gt e, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为向量 $\displaystyle x$ 关于完全规范正交系的 Fourier 展开式.

---

4、 Hilbert 空间中规范正交系完全的充要条件 (Steklov 定理): 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle M$ 是 $\displaystyle X$ 的规范正交系, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M\mbox{ 完全}\Leftrightarrow \mbox{Parseval 等式在 $\displaystyle X$ 的某稠密子集 $\displaystyle A$ 上成立}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

也即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} &\exists\ A\subset X,\mathrm{ s.t.} \bar{A}=X,\ x\in A\\ \Rightarrow& \left\Vert x\right\Vert ^2=\sum_{e\in M}|\left\lt x,e\right\gt |^2. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

5、 Steklov 定理的应用: 三角函数系 $\displaystyle M$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} e_0(x)=\frac{1}{\sqrt{2}},e_1(x)=\cos x,e_2(x)=\sin x,\cdots,\atop e_{2n-1}(x)=\cos nx,e_{2n}(x)=\sin nx,\cdots \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

在 $\displaystyle L^2[0,2\pi]$ 中稠密, 且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mbox{对 }e_k(x),\mbox{ Parseval 等式成立}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

据 Steklov 定理, $\displaystyle M$ 是 $\displaystyle L^2[0,2\pi]$ 中完全规范正交系, 而 $\displaystyle f\in L^2[0,2\pi]$ $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \Rightarrow f(x)&=\sum_{k=0}^\infty \left\lt f,e_k\right\gt e_k(x)\\ &=\frac{a_0}{\sqrt{2}}+\sum_{k=1}^\infty (a_k\cos kx+b_k\sin kx), \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

其中等号右端级数是指在 $\displaystyle L^2[0,2\pi]$ 中平均平方收敛.

09.3.7. Hilbert 空间中完全规范正交系的存在性、Hilbert 维数

---

1、 思考.

(1)、 存在性: 非零 Hilbert 空间是否存在完全规范正交系?

(2)、 如何去得到完全规范正交系?

---

2、 Gram-Schmidt 规范正交化过程-(线性无关 $\displaystyle \to$ 规范正交): 设 $\displaystyle X$ 是内积空间, $\displaystyle \left\{x_1,x_2,\cdots\right\}\subset X$ 是有限或可数个线性无关的向量, 那么必有 $\displaystyle X$ 中规范正交系 $\displaystyle \left\{e_1,e_2,\cdots\right\}$, 使得对任何正整数 $n$, 有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \mathrm{span}\left\{e_1,\cdots,e_n\right\} =\mathrm{span}\left\{x_1,\cdots,x_n\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 非零 Hilbert 空间完全规范正交系的存在性: 每个非零 Hilbert 空间必有完全规范正交系.

---

4、 Hilbert 维数: 设 $X$ 是 Hilbert 空间, 则可证明 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} M,M_1\mbox{ 是 }X\mbox{ 的完全规范正交系}\Rightarrow \overline{\overline{M}}=\overline{\overline{M_1}}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 $\displaystyle X$ 的 Hilbert 维数.

(1)、 若 $\displaystyle X=\left\{0\right\}$, 则定义 $X$ 的 Hilbert 维数为 $\displaystyle 0$;

(2)、 若 $X$ 是有限维空间时, Hilbert 维数 $\displaystyle =$ 线性维数.

---

5、 内积空间间的同构: 设 $\displaystyle X$ 和 $\displaystyle \tilde{X}$ 是两个内积空间, 若存在 $\displaystyle X$ 到 $\displaystyle \tilde{X}$ 上的映射 $\displaystyle T$, 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T(\alpha x+\beta y)=&\alpha Tx+\beta Ty,\\ &\forall\ \alpha,\beta\in \mathbb{F},\ \forall\ x,y\in X;\\ \left\lt Tx,Ty\right\gt =&\left\lt x,y\right\gt ,\quad \forall\ x,y\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $X$ 与 $\displaystyle \tilde{X}$ $同构$; $\displaystyle T$ 为 $\displaystyle X$ 到 $\displaystyle \tilde{X}$ 的同构映射.

---

6、 Hilbert 空间同构的充要条件: 两个 Hilbert 空间 $\displaystyle X$ 与 $\displaystyle \tilde{X}$ 同构 $\displaystyle \Leftrightarrow$ $X$ 与 $\displaystyle \tilde{X}$ 具有相同的 Hilbert 维数.

---

7、 可分 Hilbert 空间的构造: 任何可分 Hilbert 空间比和某个 $\displaystyle \mathbb{R}^n$ 或 $\displaystyle \ell^2$ 同构.

09.4. 希尔伯特空间上的连续线性泛函

09.4.1. Riesz 表示定理

---

1、 Riesz 表示定理 (Hilbert 空间中连续线性泛函的构造): 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle f\in X'$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \exists\ |\ z\in X,\mathrm{ s.t.} &f(x)=(x,z),\forall\ x\in X,\\ &\mbox{且 }\left\Vert f\right\Vert =\left\Vert z\right\Vert . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 赋范线性空间的复共轭自同构 (映射): 设 $X, \tilde{X}$ 是两赋范线性空间, $\displaystyle T: X\to \tilde{X}$ 是满射, 若

(1)、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T(\alpha x+\beta y) =\bar{\alpha} Tx+\bar{\beta} Ty, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

$\displaystyle \forall\ \alpha,\beta\in\mathbb{F},\ \forall\ x,y\in X$;

(2)、 $\left\Vert Tx\right\Vert =\left\Vert x\right\Vert ,\ \forall\ x\in X$,

则称 $X$ 与 $\displaystyle \tilde{X}$ 复共轭同构, 称 $\displaystyle T$ 是复共轭同构映射.

(1)、 若 $\displaystyle X$, $X'$ 复共轭同构, 则称 $\displaystyle X$ 自共轭的.

(2)、 注意与 $\displaystyle \S 8.2$ 的 赋范线性空间的同构 相比较.

(3)、 $\displaystyle X$ 与 $\displaystyle \tilde{X}$ 不管同构还是复共轭同构, 我们都不加以区别, 视为同一.

---

3、 Hilbert 空间与其共轭空间复共轭同构, 而是自共轭的: $\displaystyle X=X'$.

09.4.2. Hilbert 空间中的共轭算子

---

1、 $n$ 阶复方阵 $\displaystyle A$ 有复共轭矩阵的概念: $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A=(a_{ij})\to A^\star =(b_{ij}),\quad b_{ij}=\overline{a_{ji}}, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

其满足 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt A e_i,e_j\right\gt =a_{ij}=\overline{b_{ji}} =\overline{\left\lt A^\star e_j,e_i\right\gt }=\left\lt e_i,A^\star e_j\right\gt , \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

而对 $\displaystyle \forall\ x=\sum_{i=1}^n \xi_ie_i,\ y=\sum_{j=1}^n \eta_je_j$, 有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt Ax,y\right\gt &=\sum_{i,j=1}^n \xi_i\eta_j\left\lt Ae_i,e_j\right\gt \\ &=\sum_{i,j=1}^n \xi_i\eta_j\left\lt e_i,A^\star e_j\right\gt =\left\lt x,A^\star y\right\gt . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们将以上内容推广到内积空间中去, 引入共轭算子的概念与性质.

---

2、 Hilbert 空间共轭算子的存在性: 设 $X,Y$ 是两个 Hilbert 空间, $\displaystyle A\in \mathscr{B}(X, Y)$, 那么存在唯一的 $A^\star \in \mathscr{B}(Y, X)$ 使得 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt Ax,y\right\gt =\left\lt x,A^\star y\right\gt ,\quad \forall\ x\in X,\ \forall\ y\in Y, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

且 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert A^\star \right\Vert =\left\Vert A\right\Vert . \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

我们称 $\displaystyle A^\star$ 为 $\displaystyle A$ 的 Hilbert 共轭算子, 简称共轭算子.

---

3、 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt Ax,y\right\gt &=\left\lt x,A^\star y\right\gt ,\ \forall\ x,y\in X;\\ \left\lt x,Ay\right\gt &=\overline{\left\lt Ay,x\right\gt } =\overline{\left\lt y,A^\star x\right\gt } =\left\lt A^\star x,y\right\gt ,\ \forall\ x,y\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 共轭算子的性质:

(1)、 $\displaystyle (A^\star )^\star =A^\star$,

(2)、 $(\alpha A)^\star =\bar{\alpha} A^\star$, $(A+B)^\star =A^\star +B^\star$,

(3)、 $(AB)^\star =(BA)^\star$.

(4)、 $\left\Vert A^\star A\right\Vert =\left\Vert AA^\star \right\Vert =\left\Vert A\right\Vert ^2$, 而 $A^\star A=0\Leftrightarrow A=0$.

09.5. 自伴算子、酉算子和正规算子

09.5.1. 引论

---

1、 高等代数中我们有 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \begin{array}{cccc} \mbox{实}&\mbox{实对称矩阵} &\mbox{正交矩阵} \\ &\uparrow&\uparrow\\ &(A^T=A)&(A^TA=I)\\ \hline \mbox{复}$&\mbox{Hermite 矩阵} & \mbox{酉矩阵} \\ &\uparrow&\uparrow\\ &(A^\star =A)&(A^\star A=I) \end{array} \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 任何一个实矩阵都可以唯一分解成一个实对称矩阵和实反对称矩阵的和, 即 $\mathbb{R}^n=V_1\oplus V_2$, $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} V_1&=\left\{A\in \mathbb{R}^{n\times n};\ A^T=A\right\},\\ V_2&=\left\{A\in\mathbb{R}^{n\times n};\ A^T=-A\right\}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 本节将上述内容推广到内积空间中去.

09.5.2. Hilbert 空间的自伴算子, 正规算子和酉算子

---

1、 Hilbert 空间的自伴算子, 正规算子和酉算子: 设 $X$ 是 Hilbert 空间, $\displaystyle T\in \mathscr{B}(X,X)$,

(1)、 若 $T^\star =T$, 即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\lt Tx,y\right\gt =\left\lt x,Ty\right\gt ,\quad \forall\ x,y\in X, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

则称 $T$ 为 $\displaystyle X$ 上的自伴算子;

(2)、 若 $\displaystyle T^\star T=TT^\star$, 则称 $T$ 为 $\displaystyle X$ 上的正规算子;

(3)、 若 $\displaystyle T$ 是一一映射, 且 $\displaystyle T^\star =T^{-1}$ $\Leftrightarrow T^\star T=TT^\star =I$, 则称 $\displaystyle T$ 为 $\displaystyle X$ 上的酉算子.

---

2、 注.

(1)、 自伴算子是实对称矩阵, Hermite 矩阵的推广.

(2)、 正规算子是正规矩阵的推广.

(3)、 酉算子是正交矩阵, 酉矩阵的推广.

09.5.3. 各算子间的关系

---

1、 自伴算子是正规算子.

---

2、 酉算子是正规算子.

---

3、 正规算子不一定是酉算子或自伴算子.

09.5.4. 复内积空间中有界线性算子为零的充要条件

---

1、 设 $\displaystyle X$ 是复内积空间, $\displaystyle T\in \mathscr{B}(X, X)$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T=0\Leftrightarrow \left\lt Tx,x\right\gt =0,\ \forall\ x\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

09.5.5. 自伴算子的性质

---

1、 设 $X$ 是复 Hilbert 空间, $\displaystyle T\in \mathscr{B}(X, X)$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T\mbox{ 自伴}\Leftrightarrow \left\lt Tx,x\right\gt \in\mathbb{R},\ \forall x\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 设 $X$ 是 Hilbert 空间, $\displaystyle T_1,T_2: X\to X$ 自伴, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T_1\cdot T_2\mbox{ 自伴}\Leftrightarrow T_1\cdot T_2=T_2\cdot T_1. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

3、 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle T_n: X\to X$ 自伴, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \lim_{n\to\infty}T_n=T\Rightarrow T\mbox{ 自伴}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 复 Hilbert 空间中有界算子的 Descarts 分解: 设 $\displaystyle X$ 是复 Hilbert 空间, $\displaystyle T\in \mathscr{B}(X, X)$, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} A=\frac{T+T^\star }{2},\quad B=\frac{T-T^\star }{2\mathrm{ i}}\mbox{ 自伴, 且 } T=A+\mathrm{ i} B, \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

称为 $T$ 的 Descarts 分解, $\displaystyle A,B$ 称为 $\displaystyle T$ 的实部与虚部.

09.5.6. 酉算子的性质

设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle U,V,U_n: X\to X$ 是酉算子, 则

---

1、 酉算子是保范算子, 也即 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} \left\Vert Ux\right\Vert =\left\Vert x\right\Vert ,\quad \forall\ x\in X. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 保范算子未必是酉算子.

---

3、 满的保范算子是酉算子: 设 $\displaystyle X$ 是 Hilbert 空间, $\displaystyle T\in \mathscr{B}(X\to X)$, 则设 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T\mbox{ 是酉算子}\Leftrightarrow T\mbox{ 是满的保范算子}. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

4、 酉算子的范数为 $1$: 当 $X\neq\left\{0\right\}$ 时, $\displaystyle \left\Vert U\right\Vert =1$.

---

5、 酉算子的逆还是酉算子: $U^{-1}$ 是酉算子.

---

6、 酉算子的乘积还是酉算子: $\displaystyle UV$ 是酉算子.

---

7、 酉算子的极限还是酉算子: $\displaystyle \lim_{n\to\infty}U_n=A\Rightarrow A$ 是酉算子.

09.5.7. 正规算子的性质

设 $\displaystyle X$ 是复 Hilbert 空间, $\displaystyle T\in\mathscr{B}(X\to X)$, 则

---

1、 $T=A+\mathrm{ i} B$ 为 $\displaystyle T$ 的 Descarts 分解, 则 $\tiny\boxed{@跟锦数学微信公众号}$

$$\begin{aligned} T\mbox{ 正规}\Leftrightarrow AB=BA. \tiny\boxed{\begin{array}{c}\mbox{跟锦数学微信公众号}\\\mbox{www.zhangzujin.cn}\end{array}}\end{aligned}$$

---

2、 $\displaystyle T$ 正规 $\Leftrightarrow \left\Vert T^\star x\right\Vert =\left\Vert Tx\right\Vert ,\ \forall\ x\in X$.

Eluer16